题目内容
19.雾霾天气对城市环境造成很大影响,按照国家环保部发布的标准:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测,抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据,制成茎叶图如图1: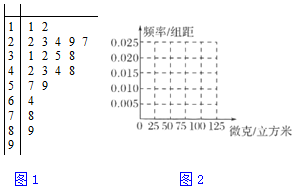
(Ⅰ)完成如下频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图如图2;
| 组别 | PM2.5浓度(微粒、立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
分析 (Ⅰ)由已知先完成频率分布表,再由频率分布表画出频率分布直方图.
(Ⅱ)设PM2.5的24小时平均浓度在(50,75]内的三天记为A1,A2,A3,PM2.5的24小时平均浓度在(75,100)内的两天记为B1,B2,5天任取2天的情况有${C}_{5}^{2}$=10种,由此能求出恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
解答 解:(Ⅰ)频率分布表为:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |

(Ⅱ)设PM2.5的24小时平均浓度在(50,75]内的三天记为A1,A2,A3,
PM2.5的24小时平均浓度在(75,100)内的两天记为B1,B2,
∴5天任取2天的情况有${C}_{5}^{2}$=10种,
其中符合条件的有:A1B1,A1B2,A2B1,A2B2,A3B1,A3B2共6种,
∴从5天中随机抽取2天,恰好有一天超过75微克/立方米的概率P=$\frac{3}{5}$.
点评 本题主要考查频率分布表、古典概型、统计等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.在△ABC中,a,b,c分别是角A,B,C的对边,若(b-$\frac{6}{5}$c)sinB+csinC=asinA,则sinA=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
7.设函数f(x)=x-|x+2|-|x-3|-m,若?x∈R,$\frac{1}{m}$-4≥f(x)恒成立.
(1)求m的取值范围;
(2)求证:log(m+1)(m+2)>log(m+2)(m+3)
(1)求m的取值范围;
(2)求证:log(m+1)(m+2)>log(m+2)(m+3)
14.已知a=log0.50.3,b=log30.5,c=0.50.3,则a,b,c的大小关系是( )
| A. | a>c>b | B. | c>a>b | C. | c>b>a | D. | b>c>a |
11.已知复数z满足z(1-i)2=1+i (i为虚数单位),则|z|为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
9.将函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{3}$个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在$[{0,\frac{π}{2}}]$的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |