题目内容
12.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b=acosC+$\frac{\sqrt{3}}{3}$csinA.(Ⅰ)求角A的大小;
(Ⅱ)若△ABC且的面积为$\sqrt{3}$,且AB边上的中线长为$\sqrt{2}$,求边长b,c.
分析 (Ⅰ)根据正弦定理和两角和的正弦公式可得tanA=$\sqrt{3}$,即可求出,
(Ⅱ)根据三角形的面积公式可得bc=4,①,再根据余弦定理可得b2+$\frac{{c}^{2}}{4}$-$\frac{1}{2}$bc=2,②,联立方程组解得即可
解答 解:(Ⅰ)∵b=acosC+$\frac{\sqrt{3}}{3}$csinA,
由正弦定理得sinB=sinAcosC+$\frac{\sqrt{3}}{3}$sinCsinA,
∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+cosAsinC=sinAcosC+$\frac{\sqrt{3}}{3}$sinCsinA,
∴cosAsinC=$\frac{\sqrt{3}}{3}$sinCsinA,
∵sinC≠0,
∴tanA=$\sqrt{3}$,
∵0<A<π,
∴A=$\frac{π}{3}$,
(Ⅱ)由(Ⅰ)知,sinA=$\frac{\sqrt{3}}{2}$,
由S△ABC=$\frac{1}{2}$bcsin$\frac{π}{3}$=$\sqrt{3}$,得bc=4,①,
设D是AB边的中点,且AB边上的中线长为$\sqrt{2}$,
在△ADC中,由余弦定理得($\sqrt{2}$)2=b2+($\frac{c}{2}$)2-2b×$\frac{c}{2}$cos$\frac{π}{3}$,
即b2+$\frac{{c}^{2}}{4}$-$\frac{1}{2}$bc=2,②,
联立①②解得b=$\sqrt{2}$,c=2$\sqrt{2}$
点评 此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
3.为调查高中生的数学成绩与学生自主学习时间之间的相关关系,某重点高中数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占$\frac{8}{13}$,统计成绩后,得到如下的2×2列联表:
(Ⅰ)请完成上面的2×2列联表,并判断在“犯错误概率不超过0.01”的前提下,能否认为“高中生的数学成绩与学生自主学习时间之间有相关关系”;
(Ⅱ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,若在上述9名学生中随机抽取2人,求至少1人分数不足120分的概率.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 分数大于等于120分 | 分数不足120分 | 合计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合计 | 25 | 20 | 45 |
(Ⅱ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,若在上述9名学生中随机抽取2人,求至少1人分数不足120分的概率.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
7.设函数f(x)=x-|x+2|-|x-3|-m,若?x∈R,$\frac{1}{m}$-4≥f(x)恒成立.
(1)求m的取值范围;
(2)求证:log(m+1)(m+2)>log(m+2)(m+3)
(1)求m的取值范围;
(2)求证:log(m+1)(m+2)>log(m+2)(m+3)
17.某早餐店每天制作甲、乙两种口味的糕点共n(n∈N*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理,该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下统计数据:
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列;
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数.
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
| 甲口味糕点日销量 | 48 | 49 | 50 | 51 |
| 天数 | 20 | 40 | 20 | 20 |
| 乙口味糕点日销量 | 48 | 49 | 50 | 51 |
| 天数 | 40 | 30 | 20 | 10 |
(1)记该店这两种糕点每日的总销量为X份,求X的分布列;
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数.
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
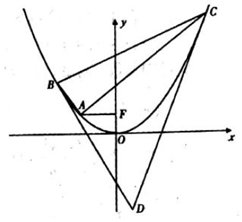 如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且$\overrightarrow{AF}$=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1,k2.
如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且$\overrightarrow{AF}$=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1,k2.