4.已知f(x)为定义在$(0,\frac{π}{2})$上的函数,f'(x)是它的导函数,且$\frac{f'(x)}{tanx}<f(x)$恒成立,则( )
| A. | $f(\frac{π}{3})<\sqrt{3}f(\frac{π}{6})$ | B. | $f(\frac{π}{6})<\sqrt{2}f(\frac{π}{4})$ | C. | $f(\frac{π}{3})<f(\frac{π}{4})$ | D. | $f(\frac{π}{4})<\sqrt{3}f(\frac{π}{3})$ |
3.已知点P(x,y)满足$|x|-1≤y≤\sqrt{1-{{|x|}^2}},O$为坐标原点,则使$|{PO}|≥\frac{{\sqrt{2}}}{2}$的概率为( )
| A. | $\frac{π}{π+2}$ | B. | $\frac{π}{π+4}$ | C. | $\frac{2}{π+1}$ | D. | $\frac{2}{π+2}$ |
2.已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,且侧棱AA1⊥平面ABC,若AB=AC=3,∠BAC=$\frac{2π}{3},A{A_1}$=8,则球的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 104π |
1.在平面直角坐标系xOy中,以(-2,0)为圆心且与直线(3m+1)x+(1-2m)y-5=0(m∈R)相切的所有圆中,面积最大的圆的标准方程是( )
| A. | (x+2)2+y2=16 | B. | (x+2)2+y2=20 | C. | (x+2)2+y2=25 | D. | (x+2)2+y2=36 |
20.为了得到函数$y=2sin(x+\frac{π}{6})cos(x+\frac{π}{6})$的图象,只需把函数y=sin2x的图象上所有的点( )
0 239046 239054 239060 239064 239070 239072 239076 239082 239084 239090 239096 239100 239102 239106 239112 239114 239120 239124 239126 239130 239132 239136 239138 239140 239141 239142 239144 239145 239146 239148 239150 239154 239156 239160 239162 239166 239172 239174 239180 239184 239186 239190 239196 239202 239204 239210 239214 239216 239222 239226 239232 239240 266669
| A. | 向左平行移动$\frac{π}{12}$个单位长度 | B. | 向右平行移动$\frac{π}{12}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
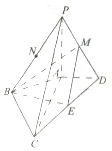 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.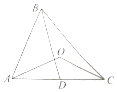 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.