15．已知f'=0.函数f处的切线的斜率为3.数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn.则S2017的值为( )A．$\frac{2017}{2018}$——青夏教育精英家教网——

15．已知f'（x）=2x+m，且f（0）=0，函数f（x）的图象在点A（1，f（1））处的切线的斜率为3，数列$\left\{{\frac{1}{f（n）}}\right\}$的前n项和为S_n，则S₂₀₁₇的值为（　　）

$\frac{2017}{2018}$

$\frac{2014}{2015}$

$\frac{2015}{2016}$

$\frac{2016}{2017}$

14．已知$cos（{α-\frac{π}{3}}）=-\frac{1}{2}$，则$sin（{\frac{π}{6}+α}）$的值等于（　　）

$\frac{\sqrt{3}}{2}$

$-\frac{{\sqrt{3}}}{2}$

13．已知z=m-1+（m+2）i在复平面内对应的点在第二象限，则实数m的取值范围是（　　）

（-∞，-2）

12．为了解600名学生的视力情况，采用系统抽样的方法，从中抽取容量为20的样本，则需要分成几个小组进行抽取（　　）

11．若集合A={x|x-x²＞0}，B={x|（x+1）（m-x）＞0}，则“m＞1”是“A∩B≠∅”的（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分也不必要条件

如图，在几何体ABCDEF中，底面ABCD为矩形，EF∥CD，CD⊥EA，CD=2EF=2，ED=$\sqrt{3}$．M为棱FC上一点，平面ADM与棱FB交于点N．
（Ⅰ）求证：ED⊥CD；
（Ⅱ）求证：AD∥MN；
（Ⅲ）若AD⊥ED，试问平面BCF是否可能与平面ADMN垂直？若能，求出$\frac{FM}{FC}$的值；若不能，说明理由．

9．设{a_n}是首项为1，公差为2的等差数列，{b_n}是首项为1，公比为q的等比数列．记c_n=a_n+b_n，n=1，2，3，…．
（1）若{c_n}是等差数列，求q的值；
（2）求数列{c_n}的前n项和S_n．

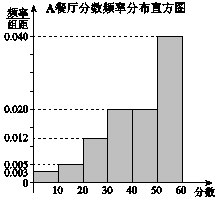某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：

B餐厅分数频数分布表
分数区间	频数
[0，10）	2
[10，20）	3
[20，30）	5
[30，40）	15
[40，50）	40
[50，60]	35

（Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
（Ⅱ）从对B餐厅评分在[0，20）范围内的人中随机选出2人，求2人中恰有1人评分在[0，10）范围内的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

7．已知函数$f（x）=tan（x+\frac{π}{4}）$．
（Ⅰ）求f（x）的定义域；
（Ⅱ）设β是锐角，且$f（β）=2sin（β+\frac{π}{4}）$，求β的值．

6．设a，b≠0，则“a＞b”是“$\frac{1}{a}＜\frac{1}{b}$”的（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分也不必要条件

0 239029 239037 239043 239047 239053 239055 239059 239065 239067 239073 239079 239083 239085 239089 239095 239097 239103 239107 239109 239113 239115 239119 239121 239123 239124 239125 239127 239128 239129 239131 239133 239137 239139 239143 239145 239149 239155 239157 239163 239167 239169 239173 239179 239185 239187 239193 239197 239199 239205 239209 239215 239223 266669