题目内容
10. 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.(Ⅰ)求证:ED⊥CD;
(Ⅱ)求证:AD∥MN;
(Ⅲ)若AD⊥ED,试问平面BCF是否可能与平面ADMN垂直?若能,求出$\frac{FM}{FC}$的值;若不能,说明理由.
分析 (Ⅰ)证明:CD⊥平面EAD,即可证明ED⊥CD;
(Ⅱ)证明AD∥平面FBC,即可证明:AD∥MN;
(Ⅲ)若使平面ADMN⊥平面BCF,则DM⊥平面BCF,所以DM⊥FC,可得DF=DC=2.若使DM⊥FC能成立,则M为FC的中点.
解答 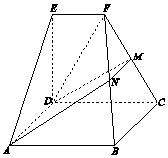 (Ⅰ)证明:因为ABCD为矩形,所以VD⊥AD.[(1分)]
(Ⅰ)证明:因为ABCD为矩形,所以VD⊥AD.[(1分)]
又因为CD⊥EA,[(2分)]
所以CD⊥平面EAD.[(3分)]
所以ED⊥CD.[(4分)]
(Ⅱ)证明:因为ABCD为矩形,所以AD∥BC,[(5分)]
所以AD∥平面FBC.[(7分)]
又因为平面ADMN∩平面FBC=MN,
所以AD∥MN.[(8分)]
(Ⅲ)解:平面ADMN与平面BCF可以垂直.证明如下:[(9分)]
连接DF.因为AD⊥ED,AD⊥CD.ED∩CD=D,
所以AD⊥平面CDEF.[(10分)]
所以AD⊥DM.
因为AD∥MN,所以DM⊥MN.[(11分)]
因为平面ADMN∩平面FBC=MN,
若使平面ADMN⊥平面BCF,
则DM⊥平面BCF,所以DM⊥FC.[(12分)]
在梯形CDEF中,因为EF∥CD,DE⊥CD,CD=2EF=2,ED=$\sqrt{3}$,
所以DF=DC=2.
所以若使DM⊥FC能成立,则M为FC的中点.
所以$\frac{FM}{FC}$=$\frac{1}{2}$.[(14分)]
点评 本题考查线面平行的判定与性质,考查线面垂直、面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
1.已知A、B为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右顶点,F1,F2为其左右焦点,双曲线的渐近线上一点P(x0,y0)(x0<0,y0>0),满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,且∠PBF1=45°,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}$ |
18.设命题p:?x>0,log2x<2x+3,则¬p为( )
| A. | ?x>0,log2x≥2x+3 | B. | ?x>0,log2x≥2x+3 | C. | ?x>0,log2x<2x+3 | D. | ?x<0,log2x≥2x+3 |
5.若抛物线y2=ax的焦点到其准线的距离是2,则a=( )
| A. | ±1 | B. | ±2 | C. | ±4 | D. | ±8 |
15.已知f'(x)=2x+m,且f(0)=0,函数f(x)的图象在点A(1,f(1))处的切线的斜率为3,数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2017的值为( )
| A. | $\frac{2017}{2018}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
1.已知函数f(x)=cos$\frac{1}{2}$x的图象向右平移π个单位得到函数y=g(x)的图象,则g($\frac{π}{3}$)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
2.城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表:
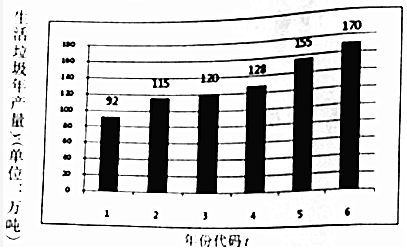
注1:年份代码1~6分别对应年份2011~2016
注2:参与度=$\frac{参加垃圾分类人数}{调查人数}$×100%
参与度的年增加值=年末参与度-年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为$\widehat{y}$=14.8t+$\widehat{a}$,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题:
①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?

| 2016年初 | 2016年末 | |
| 社区A | 539 | 568 |
| 社区B | 543 | 585 |
| 社区C | 568 | 600 |
| 社区D | 496 | 513 |
注2:参与度=$\frac{参加垃圾分类人数}{调查人数}$×100%
参与度的年增加值=年末参与度-年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为$\widehat{y}$=14.8t+$\widehat{a}$,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题:
①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?