题目内容
13.已知z=m-1+(m+2)i在复平面内对应的点在第二象限,则实数m的取值范围是( )| A. | (-1,2) | B. | (-2,1) | C. | (1,+∞) | D. | (-∞,-2) |
分析 利用复数的几何意义、不等式的解法即可得出.
解答 解:z=m-1+(m+2)i在复平面内对应的点在第二象限,
∴m-1<0,m+2>0,解得-2<m<1.
则实数m的取值范围是(-2,1).
故选:B
点评 本题考查了复数的几何意义、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.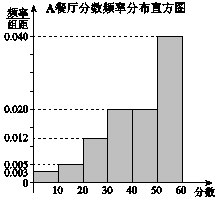 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
(Ⅰ)在抽样的100人中,求对A餐厅评分低于30的人数;
(Ⅱ)从对B餐厅评分在[0,20)范围内的人中随机选出2人,求2人中恰有1人评分在[0,10)范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:| B餐厅分数频数分布表 | |
| 分数区间 | 频数 |
| [0,10) | 2 |
| [10,20) | 3 |
| [20,30) | 5 |
| [30,40) | 15 |
| [40,50) | 40 |
| [50,60] | 35 |
(Ⅱ)从对B餐厅评分在[0,20)范围内的人中随机选出2人,求2人中恰有1人评分在[0,10)范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
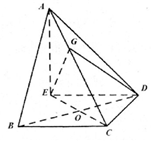 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.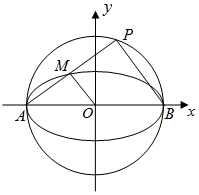 已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.
已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.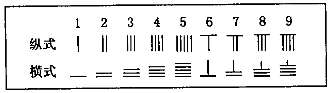
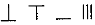 ,则5288用算筹式可表示为
,则5288用算筹式可表示为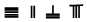 .
.