题目内容
14.已知$cos({α-\frac{π}{3}})=-\frac{1}{2}$,则$sin({\frac{π}{6}+α})$的值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 由已知利用诱导公式即可计算得解.
解答 解:∵$cos({α-\frac{π}{3}})=-\frac{1}{2}$,可得:cos($\frac{π}{3}$-α)=-$\frac{1}{2}$,
∴sin[$\frac{π}{2}$-($\frac{π}{3}$-α)]=sin($\frac{π}{6}$+α)=-$\frac{1}{2}$.
故选:D.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
5.若集合A={x|x(x-1)<2},且A∪B=A,则集合B可能是( )
| A. | {-1,2} | B. | {0,1} | C. | {-1,0} | D. | {0,2} |
2.已知集合A={x∈R|-1<x<1},B={x∈R|x•(x-2)<0},那么A∩B=( )
| A. | {x∈R|0<x<1} | B. | {x∈R|0<x<2} | C. | {x∈R|-1<x<0} | D. | {x∈R|-1<x<2} |
9.设{an}是首项为1,公差为2的等差数列,{bn}是首项为1,公比为q的等比数列.记cn=an+bn,n=1,2,3,….
(1)若{cn}是等差数列,求q的值;
(2)求数列{cn}的前n项和Sn.
(1)若{cn}是等差数列,求q的值;
(2)求数列{cn}的前n项和Sn.
8.不论角α的终边位置如何,在单位圆中作三角函数线时,下列说法正确的是( )
| A. | 总能分别作出正弦线、余弦线、正切线 | |
| B. | 总能分别作出正弦线、余弦线、正切线,但可能不只一条 | |
| C. | 正弦线、余弦线、正切线都可能不存在 | |
| D. | 正弦线、余弦线总存在,但正切线不一定存在 |
6.已知随机变量X+Y=10,若X~B(10,0.6),则E(Y),D(Y)分别是( )
| A. | 6和2.4 | B. | 4和5.6 | C. | 4和2.4 | D. | 6和5.6 |
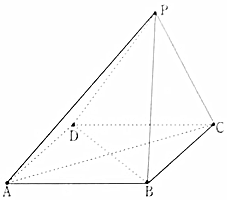 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.