3.某供货商计划将某种大型节日商品分别配送到甲、乙两地销售.据以往数据统计,甲、乙两地该商品需求量的频率分布如下:
甲地需求量频率分布表示:
乙地需求量频率分布表:
以两地需求量的频率估计需求量的概率
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
甲地需求量频率分布表示:
| 需求量 | 4 | 5 | 6 |
| 频率 | 0.5 | 0.3 | 0.2 |
| 需求量 | 3 | 4 | 5 |
| 频率 | 0.6 | 0.3 | 0.1 |
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
18.已知一个圆锥底面半径为1,母线长为3,则该圆锥内切球的表面积为( )
| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
17.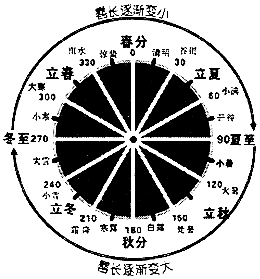 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 四尺五寸 |
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则下列关系可以成立的而是( )
| A. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$ | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$ |
15.执行如图的程序框图,则输出的结果为( )
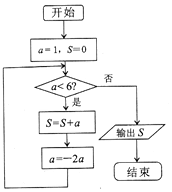

| A. | 15 | B. | 3 | C. | -11 | D. | -5 |
14.已知集合M={x|1<x≤3},若N={x|0≤x<2},则M∪N=( )
0 238995 239003 239009 239013 239019 239021 239025 239031 239033 239039 239045 239049 239051 239055 239061 239063 239069 239073 239075 239079 239081 239085 239087 239089 239090 239091 239093 239094 239095 239097 239099 239103 239105 239109 239111 239115 239121 239123 239129 239133 239135 239139 239145 239151 239153 239159 239163 239165 239171 239175 239181 239189 266669
| A. | {x|0≤x≤3} | B. | {x|1<x<2} | C. | {x|0≤x≤1} | D. | {x|2<x≤3} |