题目内容
1.已知函数f(x)=xlnx+x-k(x-1)在(1,+∞)内有唯一零点x0,若k∈(n,n+1),n∈Z,则n=3.分析 求导f′(x)=1+lnx+1-k=lnx+2-k从而分类讨论以确定函数的单调性,从而转化为最值问题求解即可.
解答 解:∵f(x)=xlnx+x-k(x-1),x∈(1,+∞),
∴f′(x)=1+lnx+1-k=lnx+2-k,
当k≤2时,f′(x)>0恒成立,
∴f(x)在(1,+∞)上单调递增,且f(x)>f(1)=1,
∴f(x)在(1,+∞)上没有零点,
当k>2时,令f′(x)>0,解得x>ek-2,函数f(x)单调递增,
令f′(x)<0,解得1<x<ek-2,函数f(x)单调递减,
∴f(x)min=f(ek-2)=(k-2)ek-2+ek-2-kek-2+k=-ek-2+k,
∵f(x)=xlnx+x-k(x-1)在(1,+∞)内有唯一零点x0,
∴f(x0)=f(ek-2)=0,
即-ek-2+k=0,
令g(k)=-ek-2+k,k>2.
∴g′(k)=-ek-2<0恒成立,
∴g(k)在(2,+∞)上单调递减,
∵g(3)=-e+3>0,g(4)=-e2+4<0,
∴g(3)•g(4)<0,
∴k∈(3,4),
∵k∈(n,n+1),n∈Z,
∴n=3,
故答案为:3.
点评 本题考查函数与导数等基本知识,考查推理论证能力和运算求解能力,考查函数与方程的思想、化归与转化的思想、数形结合的思想,考查运用数学知识分析和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知i是虚数单位,若复数z满足z2=-4,则$\frac{1}{z}$=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$i | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{2}$i |
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则下列关系可以成立的而是( )
| A. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$ | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$ |
6.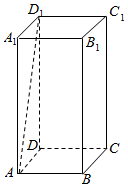 如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )
 如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{4}{5}$ |
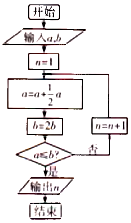 《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )
《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )