8.已知实数x,y满足$\left\{\begin{array}{l}2x-y-5≥0\\ 2x+y-3≥0\\ y≤x\end{array}\right.$,则z=-3x-y的最大值为( )
| A. | -19 | B. | -7 | C. | -5 | D. | -4 |
7.下列函数中,以$\frac{π}{2}$为最小正周期的偶函数是( )
| A. | $y=cos({2x+\frac{π}{2}})$ | B. | y=sin22x-cos22x | C. | y=sin2x+cos2x | D. | y=sin2xcos2x |
6.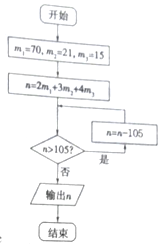 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
5.“log2a>log2b”是“${({\frac{1}{3}})^a}<{({\frac{1}{3}})^b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.若复数$\frac{m+i}{1-i}$为纯虚数(i为虚数单位),则实数m等于( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
3.设集合A={x|x2-3x+2<0},B={x|1<x<3},则( )
| A. | A=B | B. | A?B | C. | A⊆B | D. | A∩B=∅ |
2.若关于x的方程(x-2)2ex+ae-x=2a|x-2|(e为自然对数的底数)有且仅有6个不等的实数解,则实数a的取值范围是( )
| A. | ($\frac{{e}^{2}}{2e-1}$,+∞) | B. | (e,+∞) | C. | (1,e) | D. | (1,$\frac{{e}^{2}}{2e-1}$) |
1.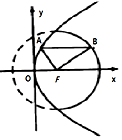 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A. | (6,10) | B. | (8,12) | C. | [6,8] | D. | [8,12] |
20.某条公共汽车线路收支差额y与乘客量x的函数关系如图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

0 238963 238971 238977 238981 238987 238989 238993 238999 239001 239007 239013 239017 239019 239023 239029 239031 239037 239041 239043 239047 239049 239053 239055 239057 239058 239059 239061 239062 239063 239065 239067 239071 239073 239077 239079 239083 239089 239091 239097 239101 239103 239107 239113 239119 239121 239127 239131 239133 239139 239143 239149 239157 266669

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |