题目内容
7.下列函数中,以$\frac{π}{2}$为最小正周期的偶函数是( )| A. | $y=cos({2x+\frac{π}{2}})$ | B. | y=sin22x-cos22x | C. | y=sin2x+cos2x | D. | y=sin2xcos2x |
分析 利用诱导公式、二倍角公式化简函数的解析式,再利用三角函数的奇偶性、周期性,得出结论.
解答 解:∵cos(2x+$\frac{π}{2}$)=-sin2x,是奇函数,故排除A;
∵y=sin22x-cos22x=-cos4x,是偶函数,且$T=\frac{π}{2}$,故B满足条件;
∵y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)是非奇非偶函数,故排除C;
∵y=sin2xcos2x=$\frac{1}{2}$sin4x是奇函数,故排除D,
故选:B.
点评 本题主要考查诱导公式、二倍角公式、三角函数的奇偶性、周期性,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
17.如图,正方形ABCD中,P,Q分别是边BC,CD的中点,若$\overrightarrow{AC}$=x$\overrightarrow{AP}$+y$\overrightarrow{BQ}$,则xy=( )
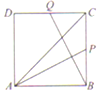

| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{12}{25}$ |
18.设x,y满足约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a,b>0)的最大值是12,则a2+b2的最小值是( )
| A. | $\frac{6}{13}$ | B. | $\frac{36}{5}$ | C. | $\frac{36}{13}$ | D. | $\frac{6}{5}$ |
15.已知△ABC是边长为4的等边三角形,D、P是△ABC内部两点,且满足$\overrightarrow{AD}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{AP}=\overrightarrow{AD}+\frac{1}{8}\overrightarrow{BC}$,则△ADP的面积为( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
2.若关于x的方程(x-2)2ex+ae-x=2a|x-2|(e为自然对数的底数)有且仅有6个不等的实数解,则实数a的取值范围是( )
| A. | ($\frac{{e}^{2}}{2e-1}$,+∞) | B. | (e,+∞) | C. | (1,e) | D. | (1,$\frac{{e}^{2}}{2e-1}$) |
12.球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切,点M为棱DD1的中点,则平面ACM截球O所得截面的面积为( )
| A. | $\frac{4π}{3}$ | B. | π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
19.在区间[-3,3]内随机取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
16.若${(x-1)^8}=1+{a_1}x+{a_2}{x^2}+…+{a_8}{x^8}$,则a5=( )
| A. | 56 | B. | -56 | C. | 35 | D. | -35 |