4.在一段时间内,某种商品的价格x元和需求量y件之间的一组数据为:
且知x与y具有线性相关关系,求出y对x的线性回归方程,并说明拟合效果的好坏.
| x(元) | 14 | 16 | 18 | 20 | 22 |
| y(件) | 12 | 10 | 7 | 5 | 3 |
2.为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6根弹簧进行测量,得到如下数据:
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程.
( 其中 $\begin{array}{l}b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}$)
0 238953 238961 238967 238971 238977 238979 238983 238989 238991 238997 239003 239007 239009 239013 239019 239021 239027 239031 239033 239037 239039 239043 239045 239047 239048 239049 239051 239052 239053 239055 239057 239061 239063 239067 239069 239073 239079 239081 239087 239091 239093 239097 239103 239109 239111 239117 239121 239123 239129 239133 239139 239147 266669
| x (g) | 5 | 10 | 15 | 20 | 25 | 30 |
| y (cm) | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程.
( 其中 $\begin{array}{l}b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}$)
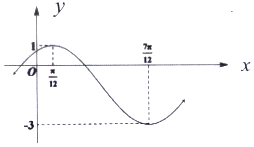 已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.