7．某生物产品，每一生产周期成本为10万元，此产品的产量受气候影响、价格受市场影响均具有随机性，且互不影响，其具体情况如表：
（Ⅰ）设X表示1生产周期此产品的利润，求X的分布列；
（Ⅱ）若连续3生产周期，求这3生产周期中至少有2生产周期的利润不少于20万元的概率．
| 产量（吨） | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格（万元/吨） | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
（Ⅱ）若连续3生产周期，求这3生产周期中至少有2生产周期的利润不少于20万元的概率．
4．
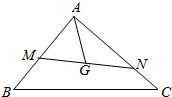如图所示，已知点G是△ABC的重心，过点G作直线与AB，AC两边分别交于M，N两点，且$\overrightarrow{AM}$=x$\overrightarrow{AB}$，$\overrightarrow{AN}$=y$\overrightarrow{AC}$，则x+2y的最小值为（ ）
如图所示，已知点G是△ABC的重心，过点G作直线与AB，AC两边分别交于M，N两点，且$\overrightarrow{AM}$=x$\overrightarrow{AB}$，$\overrightarrow{AN}$=y$\overrightarrow{AC}$，则x+2y的最小值为（ ）| A． | 2 | B． | $\frac{1}{3}$ | C． | $\frac{{3+2\sqrt{2}}}{3}$ | D． | $\frac{3}{4}$ |
3．已知不等式组$\left\{\begin{array}{l}{x+y-2\sqrt{2}≥0}\\{x≤2\sqrt{2}}\\{y≤2\sqrt{2}}\end{array}\right.$表示平面区域Ω，过区域Ω中的任意一个点P，作圆x2+y2=1的两条切线且切点分别为A，B，当△PAB的面积最小时，cos∠APB的值为（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
2．已知f（x）是偶函数，它在[0，+∞）上是减函数，若f（lgx）＞f（2），则x的取值范围是（ ）
| A． | $（\frac{1}{100}，1）$ | B． | （0，$\frac{1}{100}$）∪（1，+∞） | C． | $（\frac{1}{100}，100）$ | D． | （0，1）∪（100，+∞） |
1．若a，b∈R，命题p：直线y=ax+b与圆x2+y2=1相交；命题$q：a＞\sqrt{{b^2}-1}$，则p是q的 （ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
20．
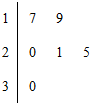某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则至少有1名优秀工人的概率为
（ ）
某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则至少有1名优秀工人的概率为 （ ）
| A． | $\frac{8}{15}$ | B． | $\frac{4}{9}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{9}$ |
19．已知全集U=R，集合A={x|y=lg（x-1）}，集合$B=\left\{{\left.y\right|y}\right.=\sqrt{{x^2}+2x+5}\left.{\;}\right\}$，则A∩B=（ ）
0 224617 224625 224631 224635 224641 224643 224647 224653 224655 224661 224667 224671 224673 224677 224683 224685 224691 224695 224697 224701 224703 224707 224709 224711 224712 224713 224715 224716 224717 224719 224721 224725 224727 224731 224733 224737 224743 224745 224751 224755 224757 224761 224767 224773 224775 224781 224785 224787 224793 224797 224803 224811 266669
| A． | ∅ | B． | （1，2] | C． | [2，+∞） | D． | （1，+∞） |
如图，已知抛物线y=ax2+bx+c经过O（0，0），A（4，0），B（3，$\sqrt{3}$）三点，连接AB，过点B作BC∥x轴交该抛物线于点C．