题目内容
7.某生物产品,每一生产周期成本为10万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如表:| 产量(吨) | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格(万元/吨) | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
分析 (Ⅰ)设A表示事件“产品产量为30吨”,B表示事件“作物市场价格为0.6万元/吨”,由题意P(A)=0.5,P(B)=0.4和X的可能取值,分别求概率可得分布列;
(Ⅱ)设Ci表示事件“第i生产周期利润不少于20万元”(i=1,2,3),则C1,C2,C3相互独立,可得P(Ci),由相互独立事件和互斥事件的概率公式可得.
解答 解:(Ⅰ)设A表示事件“产品产量为30吨”,B表示事件“作物市场价格为0.6万元/吨”,
则P(A)=0.5,P(B)=0.4,∵利润=产量×市场价格-成本,∴X的所有值为:
50×1-10=40,50×0.6-10=20,
30×1-10=20,30×0.6-10=8,
则P(X=40)=P($\overline{A}$)P($\overline{B}$)=(1-0.5)×(1-0.4)=0.3,
P(X=20)=P($\overline{A}$)P(B)+P(A)P($\overline{B}$)=(1-0.5)×0.4+0.5(1-0.4)=0.5,
P(X=8)=P(A)P(B)=0.5×0.4=0.2,
则X的分布列为:
| X | 40 | 20 | 8 |
| P | 0.3 | 0.5 | 0.2 |
由(Ⅰ)知,P(Ci)=P(X=40)+P(X=20)=0.3+0.5=0.8(i=1,2,3),
3生产周期的利润均不少于20的概率为P(C1C2C3)=P(C1)P(C2)P(C3)=0.83=0.512,
3生产周期的利润有2生产周期不少于20的概率为P($\overline{{C}_{1}}$C2C3)+P(C1$\overline{{C}_{2}}$C3)+P(C1C2$\overline{{C}_{3}}$)=3×0.82×0.2=0.384,
∴所求概率P=0.512+0.384=0.896
点评 本题考查概率分布列,涉及概率的加法和乘法公式,属中档题.

练习册系列答案
相关题目
2.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(2),则x的取值范围是( )
| A. | $(\frac{1}{100},1)$ | B. | (0,$\frac{1}{100}$)∪(1,+∞) | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
19.下列叙述错误的是( )
| A. | 若事件A发生的概率为P(A),则0≤P(A)≤1 | |
| B. | 系统抽样是不放回抽样,每个个体被抽到的可能性相等 | |
| C. | 线性回归直线$\hat y=\hat bx+\hat a$必过点$(\overline x,\overline y)$ | |
| D. | 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B) |
16.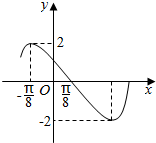 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )| A. | y=2sin(2x-$\frac{π}{4}$) | B. | y=2sin(2x-$\frac{π}{4}$)或y=2sin(2x+$\frac{3π}{4}$) | ||
| C. | y=2sin(2x+$\frac{3π}{4}$) | D. | y=2sin(2x-$\frac{3π}{4}$) |