题目内容
5.已知△ABC的角A、B、C的对边分别为a、b、c,其面积S=4$\sqrt{3}$,∠B=60°,且a2+c2=2b2;等差数列{an}中,且a1=a,公差d=b.数列{bn}的前n项和为Tn,且Tn-2bn+3=0,n∈N*.(1)求数列{an}、{bn的通项公式;
(2)设cn=$\left\{\begin{array}{l}{{a}_{n},n为奇数}\\{{b}_{n},n为偶数}\end{array}\right.$,求数列{cn}的前2n+1项和P2n+1.
分析 (1)运用三角形的面积公式和余弦定理,解得a=b=c=4,由等差数列的通项公式可得an=4n;再由数列的通项与求和的关系,可得数列{bn}为等比数列,求得bn;
(2)求得cn=$\left\{\begin{array}{l}{4n,n为奇数}\\{3•{2}^{n-1},n为偶数}\end{array}\right.$,运用数列的求和方法:分组求和,结合等差数列和等比数列的求和公式,化简整理即可得到所求和.
解答 解:(1)S=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac•$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,∴ac=16,
又 a2+c2=2b2,b2=a2+c2-2accosB,
∴b2=ac=16,∴b=4,
从而(a+c)2=a2+c2+2ac=64⇒a+c=8∴a=c=4
故可得:$\left\{{\begin{array}{l}{{a_1}=4}\\{d=4}\end{array}}\right.$,∴an=4+4(n-1)=4n;
∵Tn-2bn+3=0,∴当n=1时,b1=3,
当n≥2时,Tn-1-2bn-1+3=0,
两式相减,得bn=2bn-1,(n≥2)
∴数列{bn}为等比数列,
∴${b_n}=3•{2^{n-1}}$.
(2)cn=$\left\{\begin{array}{l}{4n,n为奇数}\\{3•{2}^{n-1},n为偶数}\end{array}\right.$,
前2n+1项和P2n+1=[4+12+…+4(2n+1)]+(6+24+…+3•22n-1)
=$\frac{[4+4(2n+1)](n+1)}{2}+\frac{6(1-{4}^{n})}{1-4}$
=22n+1+4n2+8n+2.
点评 本题考查三角形的余弦定理和面积公式的运用,考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和,考查运算能力,属于中档题.

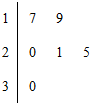 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
| A. | -3e | B. | -1 | C. | -e3 | D. | e2 |
| A. | 330° | B. | 210° | C. | 150° | D. | 30° |
| A. | (-2,0) | B. | (-1,1) | C. | (0,2) | D. | (1,3) |
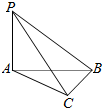 如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.
如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.