Question

3．已知不等式组$\left\{\begin{array}{l}{x+y-2\sqrt{2}≥0}\\{x≤2\sqrt{2}}\\{y≤2\sqrt{2}}\end{array}\right.$表示平面区域Ω，过区域Ω中的任意一个点P，作圆x²+y²=1的两条切线且切点分别为A，B，当△PAB的面积最小时，cos∠APB的值为（　　）

• A． $\frac{7}{8}$
• B． $\frac{1}{2}$
• C． $\frac{3}{4}$
• D． $\frac{{\sqrt{3}}}{2}$

Answer 1

分析 作出平面区域Ω和单位圆x²+y²=1，数形结合可得当P到原点距离最小时，△PAB的面积最小，由三角形的知识可得．

解答 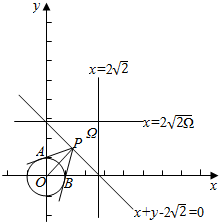解：作出平面区域Ω和单位圆x²+y²=1，l：x+y-2$\sqrt{2}$=0，
数形结合可得S_PABO=2S_△PAO=2×$\frac{1}{2}$×PA×1=PA，
设PA=x，△ABO的面积为$\frac{1}{2}$sin∠AOB=$\frac{1}{2}$•$\frac{2x}{1+{x}^{2}}$=$\frac{x}{1+{x}^{2}}$，
即有△PAB的面积为x-$\frac{x}{1+{x}^{2}}$=$\frac{{x}^{3}}{1+{x}^{2}}$，由于在X＞0上递增，
∴当P到原点距离最小时，PA最小，△PAB的面积最小，
此时PO⊥l，且|PO|=2，故∠PAO=$\frac{π}{6}$，
∴∠APB=$\frac{π}{3}$，cos∠APB=$\frac{1}{2}$，
故选：B．

点评 本题考查简单线性规划，准确作图并转化是解决问题的关键，属中档题．