题目内容
20．
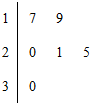某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则至少有1名优秀工人的概率为 （ ）
| A． | $\frac{8}{15}$ | B． | $\frac{4}{9}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{9}$ |
分析 由茎叶图可得工人加工的零件数，可得优秀工人数，列举法和概率公式可得．
解答 解：由茎叶图可知6名工人加工零件数为：17，19，20，21，25，30，
平均值为：$\frac{1}{6}$（17+19+20+21+25+30）=22，优秀的为25，30有2人，
从该车间6名工人中，任取2人共有15种取法：（17，19）（17，20）（17，21）（17，25）（17，30）
（19，20）（19，21）（19，25）（19，30）（20，21）（20，25）（20，30）（21，25）（21，30）（25，30）．
其中至少有1名优秀工人的共有9种取法：（17，25）（17，30）（19，25）（19，30）（20，25）（20，30）（21，25）（21，30）（25，30）．
由概率公式可得P=$\frac{9}{15}$=$\frac{3}{5}$，
故选：C．
点评 本题考查列举法计算基本事件数及事件发生的概率，涉及茎叶图的知识，属基础题．
练习册系列答案
相关题目
8．下列函数中，满足“f（x+y）=f（x）f（y）”的单调递增函数是（ ）
| A． | f（x）=x3 | B． | f（x）=lgx | C． | $f（x）={（{\frac{1}{2}}）^x}$ | D． | f（x）=3x |
9．已知实数a＞0，b＞0，函数f（x）=ax2+b满足：对任意实数x，y，有f（xy）+f（x+y）≥f（x）f（y），则实数a的取值范围是（ ）
| A． | （0，1] | B． | （0，1） | C． | （0，2） | D． | （0，2] |
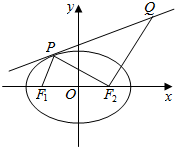已知F1，F2是椭圆$Γ：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点，椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$，P（x0，y0）是Γ上异于左右顶点的任意一点，且△PF1F2的面积的最大值为1．