向量
=（3，-4），向量|
|=2，若
•
=-5，那么向量
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知n为正偶数，用数学归纳法证明1-
+
-
+…+
-
=2(
+
+…+
)时，第一步应验证（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
A、1=2×
| ||||||||||
B、1-
| ||||||||||
C、1-
| ||||||||||
D、1-
|
在等差数列{an}中，a4=2，则前7项的和S7等于（ ）
| A、28 | B、14 | C、3.5 | D、7 |
点（x0，y0）在圆x2+y2=16内的充分不必要条件是（ ）
| A、x02+y02=16． |
| B、x02+y02＜16 |
| C、x02+y02＞16 |
| D、x02+y02＜4 |
从1，2，3…20这20个数中任取2个不同的数，则这两个数之和是3的倍数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
中心在原点，焦点在x轴上的双曲线C的离心率为2，直线l与双曲线C交于A、B两点，线段AB中点M在第一象限，并且在抛物线y2=2px（p＞0）上，且M到抛物线焦点的距离为p，则直线l的斜率为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
若x=
是f（x）=
sinωx+cosωx的图象的一条对称轴，则ω可以是（ ）
| π |
| 6 |
| 3 |
| A、4 | B、8 | C、2 | D、1 |
直线l过双曲线的右焦点，斜率为
，若l与双曲线的两个交点分别在其两支上，则双曲线的离心率的取值范围为（ ）
| 2 |
A、[
| ||
| B、（2，+∞） | ||
C、[
| ||
D、（
|
已知双曲线
-
=1(a＞0，b＞0)与抛物线y2=2px（p＞0）的交点为：A、B，A、B连线经过抛物线的焦点F，且线段AB的长等于双曲线的虚轴长，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
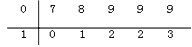如图所示的茎叶图记录了一组数据，关于这组数据给出了如下四个结论：①众数是9；②平均数10；③中位数是9或10；④方差是3.4，其中正确命题的个数是（ ）