题目内容
中心在原点,焦点在x轴上的双曲线C的离心率为2,直线l与双曲线C交于A、B两点,线段AB中点M在第一象限,并且在抛物线y2=2px(p>0)上,且M到抛物线焦点的距离为p,则直线l的斜率为( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用抛物线的定义,确定M的坐标,利用点差法将线段AB中点M的坐标代入,即可求得结论.
解答:
解:∵M在抛物线y2=2px(p>0)上,且M到抛物线焦点的距离为p,
∴M的横坐标为
,∴M(
,p)
设双曲线方程为
-
=1(a>0,b>0),A(x1,y1),B(x2,y2),则
-
=1,
-
=1
两式相减,并将线段AB中点M的坐标代入,可得
-
=0,
∴
=
=
=
=
.
故选C.
∴M的横坐标为
| p |
| 2 |
| p |
| 2 |
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
两式相减,并将线段AB中点M的坐标代入,可得
| p(x1-x2) |
| a2 |
| 2p(y1-y2) |
| b2 |
∴
| y1-y2 |
| x1-x2 |
| b2 |
| 2a2 |
| c2-a2 |
| 2a2 |
| e2-1 |
| 2 |
| 3 |
| 2 |
故选C.
点评:本题考查双曲线与抛物线的综合,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
若对一切x∈R,mx2+2mx-3<0恒成立,则实数m的取值范围为( )
| A、(-3,0) |
| B、(-3,0] |
| C、(-∞,-3] |
| D、(-∞,0] |
已知函数f(x)=mx3+3(m-1)x2-m2+1(m>0)的单调递减区间是(0,4),则m=( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
已知a,b∈R,且ab>0,则下列不等式中不正确的是( )
A、
| ||||
B、2
| ||||
| C、|a+b|≥|a-b| | ||||
| D、|a+b|<|a|+|b| |
向量
=(3,-4),向量|
|=2,若
•
=-5,那么向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
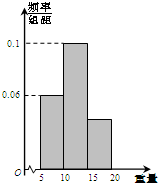 如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )
如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )