题目内容
从1,2,3…20这20个数中任取2个不同的数,则这两个数之和是3的倍数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率
专题:概率与统计
分析:所有的取法共有
=190,而满足条件的取法共有
+7×7=64,由此求得所求事件的概率.
| C | 2 20 |
| C | 2 6 |
解答:
解:所有的取法共有
=190,
1,2,3…20这20个数中,有6个是3的倍数,被3除余1的有7个,被3除余2的有7个,
取出的这两个数的和是3的倍数,包括两类:①这两个数都是3的倍数;
②这两个数中,一个被3除余1,另一个被3除余2.
故满足条件的取法共有
+7×7=64,
故要求事件的概率为 P=
=
,
故选:A.
| C | 2 20 |
1,2,3…20这20个数中,有6个是3的倍数,被3除余1的有7个,被3除余2的有7个,
取出的这两个数的和是3的倍数,包括两类:①这两个数都是3的倍数;
②这两个数中,一个被3除余1,另一个被3除余2.
故满足条件的取法共有
| C | 2 6 |
故要求事件的概率为 P=
| 64 |
| 190 |
| 32 |
| 95 |
故选:A.
点评:本题主要考查等可能事件的概率,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
公务员考试分笔试和面试,笔试的通过率为20%,最后的录取率为4%,已知某人已经通过笔试,则他最后被录取的概率为( )
| A、20% | B、24% |
| C、16% | D、4% |
定义域为R的函数f(x)=
,若关于x的方程f2(x)-af(x)+b=0有3个不同实数解x1,x2,x3,且x1<x2<x3,则下列说法错误的是( )
|
|
| A、5+b-2a=1 |
| B、b<0 |
| C、x1-x2+x3=3 |
| D、x12+x22+x32=9 |
对于R上可导的任意函数f(x),若满足
≤0,则必有( )
| 2-x |
| f′(x) |
| A、f(1)+f(3)<2f(2) |
| B、f(1)+f(3)≤2f(2) |
| C、f(1)+f(3)>2f(2) |
| D、f(1)+f(3)≥2f(2) |
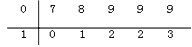 如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )
如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )