设正项等比数列{a_n}的前n项和为S_n，公比为q，若S_k-2=3，S_k=15，S_k+2=63，则q=（　　）

如图，在复平面内，点A表示复数z，则图中表示z的共轭复数的点是（　　）

已知集合M={x|log₂（x-1）＜2}，N={x|a＜x＜6}，且M∩N=（2，b），则a+b=（　　）

已知实数x、y满足约束条件

x+2y≥2 2x+y≤4 4x-y≥-1

，若

a

=（x，y），

b

=（3，-1），设z表示向量

a

在

b

方向上的投影，则z的取值范围是（　　）

已知m，l是两条不同的直线，α，β是两个不重合的平面，给出下列命题：
①若l⊥α，m∥α，则l⊥m；            
②若m∥l，m?α，则l∥α；
③若α⊥β，m?α，l?β，则m⊥l；    
④若m⊥l，m⊥α，l⊥β，则α⊥β；
其中正确命题的个数为（　　）

若不等式log₂（|x+1|+|x-2|-m）≥2恒成立，则实数m的取值范围为（　　）

抛物线x²=my上一点M（x₀，-3）到焦点的距离为5，则实数m的值为（　　）

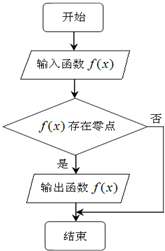执行如图所示的程序框图，若输入如下四个函数：①f（x）=sinx②f（x）=cosx③f（x）=e^|x|④f（x）=|lnx|，则输出的函数的个数为（　　）

给岀四个命题：
（1）若一个角的两边分别平行于另一个角的两边，则这两个角相等；
（2）α，β 为两个不同平面，直线a?α，直线b?α，且a∥β，b∥β，则α∥β；
（3）α，β 为两个不同平面，直线m⊥α，m⊥β  则α∥β；
（4）α，β 为两个不同平面，直线m∥α，m∥β，则α∥β．
其中正确的是（　　）

已知A、B、C三点共线，O是这条直线外一点，设

OA

=

a

，

OB

=

b

，

OC

=

c

，且存在实数m，使m

a

-3

b

-

c

=

0

成立，则点A分

BC

的比为（　　）