题目内容
已知实数x、y满足约束条件
,若
=(x,y),
=(3,-1),设z表示向量
在
方向上的投影,则z的取值范围是( )
|
| a |
| b |
| a |
| b |
A、[-
| ||||||||
| B、[-1,6] | ||||||||
C、[-
| ||||||||
D、[-
|
考点:简单线性规划,平面向量数量积的运算
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用向量投影的定义计算z的表达式,利用数形结合即可得到结论.
解答:
解:∵
=(x,y),
=(3,-1),z表示向量
在
方向上的投影,
∴z=
=
,
即y=3x-
z,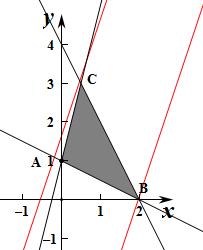
作出不等式组对应的平面区域如图:
平移直线y=3x-
z,当y=3x-
z,经过点C时直线y=3x-
z的截距最大,
此时z最小,当y=3x-
z经过点B(2,0)时,直线的截距最小,此时z最大.
由
,得
,即C(
,3),
此时最小值z=
=-
,
此时最大值z=
,
故z的取值范围是[-
,
],
故选:C.
| a |
| b |
| a |
| b |
∴z=
| ||||
|
|
| 3x-y | ||
|
即y=3x-
| 10 |

作出不等式组对应的平面区域如图:
平移直线y=3x-
| 10 |
| 10 |
| 10 |
此时z最小,当y=3x-
| 10 |
由
|
|
| 1 |
| 2 |
此时最小值z=
3×
| ||
|
| 3 | ||
2
|
此时最大值z=
| 6 | ||
|
故z的取值范围是[-
| 3 | ||
2
|
| 6 | ||
|
故选:C.
点评:本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知a≥0,函数f(x)=(x2-2ax)ex,若f(x)在[-1,1]上是单调减函数,则a的取值范围是( )
A、0<a<
| ||||
B、
| ||||
C、a≥
| ||||
D、0<a<
|
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点,△PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1•e2的取值范围是( )
A、(
| ||
B、(
| ||
C、(
| ||
| D、(0,+∞) |
给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,则α∥β;
(3)α,β 为两个不同平面,直线m⊥α,m⊥β 则α∥β;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β.
其中正确的是( )
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,则α∥β;
(3)α,β 为两个不同平面,直线m⊥α,m⊥β 则α∥β;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β.
其中正确的是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
有红、蓝、黄、绿四种颜色的球各6个,每种颜色的6个球分别标有数字1、2、3、4、5、6,从中任取3个标号不同的球,这3个颜色互不相同且所标数字互不相邻的取法种数为( )
| A、80 | B、84 | C、96 | D、104 |
设a>0,b>0,c>0下列不等关系不恒成立的是( )
A、c3+c+1>c2+
| ||||
| B、|a-b|≤|a-c|+|b-c| | ||||
C、若a+4b=1,则
| ||||
| D、ax2+bx+c≥0(x∈R) |
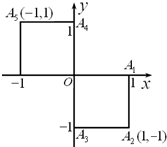 甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.