题目内容
给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,则α∥β;
(3)α,β 为两个不同平面,直线m⊥α,m⊥β 则α∥β;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β.
其中正确的是( )
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,则α∥β;
(3)α,β 为两个不同平面,直线m⊥α,m⊥β 则α∥β;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β.
其中正确的是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
考点:空间中直线与平面之间的位置关系
专题:开放型,空间位置关系与距离
分析:(1)分两种情况讨论,如图,∠1,∠2,∠3的两边互相平行,由图形可以看出∠1和∠2是邻补角,它们和∠3的关系容易知道一个相等,一个互补;
(3)由线面垂直的性质可知,两个不同平面分别垂直于同一条直线,则这两个平面相互平行;
(2)(4)列举所有情况即可得出结论.
(3)由线面垂直的性质可知,两个不同平面分别垂直于同一条直线,则这两个平面相互平行;
(2)(4)列举所有情况即可得出结论.
解答:
解:(1)如图,∠1,∠2,∠3的两边互相平行,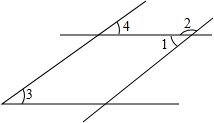 ∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠1,∠3+∠2=180°,∴这两个角相等或互补,故(1)不正确.
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,a,b相交时,α∥β,故(2)不正确;
(3)由线面垂直的性质可知,两个不同平面分别垂直于同一条直线,则这两个平面相互平行,即α∥β,正确;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β,也有可能α∩β=m,故不正确.
故选:C.
 ∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;∴∠3=∠1,∠3+∠2=180°,∴这两个角相等或互补,故(1)不正确.
(2)α,β 为两个不同平面,直线a?α,直线b?α,且a∥β,b∥β,a,b相交时,α∥β,故(2)不正确;
(3)由线面垂直的性质可知,两个不同平面分别垂直于同一条直线,则这两个平面相互平行,即α∥β,正确;
(4)α,β 为两个不同平面,直线m∥α,m∥β,则α∥β,也有可能α∩β=m,故不正确.
故选:C.
点评:本题主要考查了线面垂直与线面平行的判定定理与性质定理的应用,解题的关键是熟练掌握基本定理.

练习册系列答案
相关题目
(理)若a=
(x-1)dx,b=
(ex-1)dx,c=
(sinx-1)dx,则( )
| ∫ | 1 0 |
| ∫ | 1 0 |
| ∫ | 1 0 |
| A、a<b<c |
| B、b<c<a |
| C、c<a<b |
| D、a<c<b |
若直线m不平行于平面α,且m?α,则下列结论成立的是( )
| A、α内的所有直线与m异面 |
| B、α内的直线与m都相交 |
| C、α内存在唯一的直线与m平行 |
| D、α内不存在与m平行的直线 |
已知实数x、y满足约束条件
,若
=(x,y),
=(3,-1),设z表示向量
在
方向上的投影,则z的取值范围是( )
|
| a |
| b |
| a |
| b |
A、[-
| ||||||||
| B、[-1,6] | ||||||||
C、[-
| ||||||||
D、[-
|
设z=x+y,其中x,y满足
,当z的最大值为6时,k的值为( )
|
| A、3 | B、4 | C、5 | D、6 |
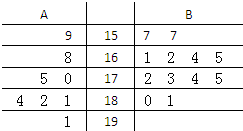 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.