题目内容
已知A、B、C三点共线,O是这条直线外一点,设
=
,
=
,
=
,且存在实数m,使m
-3
-
=
成立,则点A分
的比为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| 0 |
| BC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用三角形法则用
,
,
将
,
表示出来,根据向量共线定理,推出
,
,
满足的关系式,再有平面向量基本定理即可解题.
| a |
| b |
| c |
| BA |
| AC |
| a |
| b |
| c |
解答:
解:由向量减法的三角形法则可知,
=
-
,
=
-
∵
,
共线,
∴存在实数λ,满足
-
=λ(
-
),
即(λ+1)
-
-λ
=0,
∴3b=(3λ+3)
-3λ
,
又∵3
=m
-
,
∴根据平面向量基本定理得3λ=1,即λ=
.
故选:C.
| BA |
| a |
| b |
| AC |
| c |
| a |
∵
| BA |
| AC |
∴存在实数λ,满足
| a |
| b |
| c |
| a |
即(λ+1)
| a |
| b |
| c |
∴3b=(3λ+3)
| a |
| c |
又∵3
| b |
| a |
| c |
∴根据平面向量基本定理得3λ=1,即λ=
| 1 |
| 3 |
故选:C.
点评:本题主要考察了向量共线定理以及平面向量基本定理,难度适中,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若变量x,y满足约束条件
,则z=2x-y的最小值为( )
|
| A、4 | B、1 | C、0 | D、-1 |
 如图,在正方体ABCD-A1B1C1D1中,E为线段A1C1的中点,则异面直线DE与B1C所成角的大小为( )
如图,在正方体ABCD-A1B1C1D1中,E为线段A1C1的中点,则异面直线DE与B1C所成角的大小为( )| A、15° | B、30° |
| C、45° | D、60° |
已知a,b,c分别为△ABC内角A,B,C的对边,且a,b,c成等比数列,且B=
,则
+
=( )
| π |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
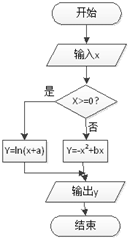 小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.
小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.