若角α的终边与单位圆交于第三象限的一点P,其横坐标为-
,则tanα=( )
| ||
| 10 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
已知函数y=2sin2(x+
),则函数的最小正周期T和它的图象的一条对称轴方程是( )
| π |
| 4 |
A、T=2π,一条对称轴方程为x=
| ||
B、T=2π,一条对称轴方程为x=
| ||
C、T=π,一条对称轴方程为x=
| ||
D、T=π,一条对称轴方程为x=
|
某几何体的三视图如图所示,则该几何体的体积是( )
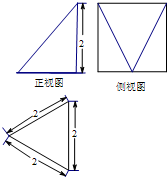

A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
在△ABC中,a=7,b=5,c=3,则cosA等于( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数f(x)=
sin2x+
cos2x的图象向右平移
个单位,再把横坐标扩大到原来的2倍得到函数y=g(x)的图象,下面结论正确的是( )
| 2 |
| 6 |
| π |
| 4 |
A、函数y=g(x)在[0,
| ||
B、函数y=g(x)图象的一个对称中心为(
| ||
C、函数y=g(x+φ)为偶函数时,其中一个φ=-
| ||
D、函数y=g(x)图象关于直线x=
|
在等差数列{an}中,a1=1,a3=5,则a5=( )
| A、3 | B、5 | C、7 | D、9 |
已知a∈R,设p:a2+3a+2≤0;q:关于x的方程x2+2x+log2a=0有实数根.则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(-x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2-a)-f(a)≥2-2a,则实数a的取值范围为( )
| A、[1,+∞) |
| B、(-∞,1] |
| C、(-∞,2] |
| D、[2,+∞) |
已知函数f(x)=x2的图象在点A(x1,f(x1))与点B(x2,f(x2))处的切线互相垂直,并交于点P,则点P的坐标可能是( )
A、(-
| ||
| B、(0,-4) | ||
| C、(2,3) | ||
D、(1,-
|
命题p:?x∈R,x2-2x+
e2xdx>0,则( )
| ∫ | 1 0 |
A、p是真命题,¬p:?x∈R,x2-2x+
| ||
B、p是假命题,¬p:?x∈R,x2-2x+
| ||
C、p是真命题,¬p:?x∈R,x2-2x+
| ||
D、p是假命题,¬p:?x∈R,x2-2x+
|