题目内容
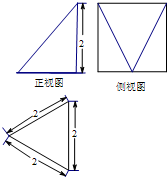
某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知：该几何体是以侧视图为底面的四棱锥，求出棱锥的底面面积和高，代入可得棱锥的体积．
解答：
解：由已知中的三视图可知：
该几何体是以侧视图为底面的四棱锥，
底面S=2×2=4，
高h=
×2=
，
故体积V=
Sh=
，
故选：B
该几何体是以侧视图为底面的四棱锥，
底面S=2×2=4，
高h=
| ||
| 2 |
| 3 |
故体积V=
| 1 |
| 3 |
4
| ||
| 3 |
故选：B
点评：本题考查的知识点是由三视图求体积，其中根据已知分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
已知函数f（x）=|lnx|，若
＞a＞b＞1，则f（a），f（b），f（c）比较大小关系正确的是（ ）
| 1 |
| c |
| A、f（c）＞f（b）＞f（a） |
| B、f（b）＞f（c）＞f（a） |
| C、f（c）＞f（a）＞f（b） |
| D、f（b）＞f（a）＞f（c） |
设函数f（x）在R上存在导数f′（x），对任意的x∈R，有f（-x）+f（x）=x2，且x∈（0，+∞）时，f′（x）＞x．若f（2-a）-f（a）≥2-2a，则实数a的取值范围为（ ）
| A、[1，+∞） |
| B、（-∞，1] |
| C、（-∞，2] |
| D、[2，+∞） |
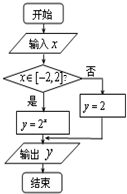
阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
甲、乙两个工人每人加工一个零件，加工为一等品的概率分别为
和
，两个零件是否被加工为一等品互相独立，则这两个工人加工的两个零件中至少有一个一等品的概率为（ ）
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个算法的程序框图如图所示，若执行该程序输出的结果为| 99 |
| 100 |
| A、i≤98？ |
| B、i≤99？ |
| C、i≤100？ |
| D、i≤101？ |