题目内容
在等差数列{an}中,a1=1,a3=5,则a5=( )
| A、3 | B、5 | C、7 | D、9 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:根据所给的等差数列的两项,做出数列的公差,根据等差数列的通项表示出第五项,代入数据得到结果.
解答:
解:∵等差数列{an}中,a1=1,a3=5,
∴d=
=2,
∴a5=a3+2d=5+4=9,
故选:D.
∴d=
| 5-1 |
| 2 |
∴a5=a3+2d=5+4=9,
故选:D.
点评:本题考查等差数列的性质,考查学生的计算能力,解题的关键是做出公差.

练习册系列答案
相关题目
计算2cos215°-1的结果为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f(x)=|lg(x+1)|,满足f(a)=f(-
),f[10(a+1)+6(b+2)-1]=4lg2,其中a,b∈R,且a<b,则a+b的值为( )
| b+1 |
| b+2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、-1 |
若角α的终边与单位圆交于第三象限的一点P,其横坐标为-
,则tanα=( )
| ||
| 10 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
某市高三数学抽样考试中,对90分以上(含90分) 的成绩进行统计,其频率分布图如图2所示,已知130~140分数段的人数为90,90~100分数段的人数为a,则图1所示程序框图的运算结果为(注:n!=1×2×3×…×n,如5!=1×2×3×4×5)( )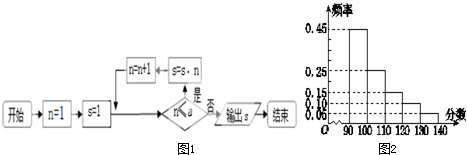

| A、800! | B、810! |
| C、811! | D、812! |
若实数x,y满足约束条件
,则z=x+2y的取值范围是( )
|
| A、[0,1] |
| B、[1,6] |
| C、[0,6] |
| D、[2,6] |