题目内容
已知函数y=2sin2(x+
),则函数的最小正周期T和它的图象的一条对称轴方程是( )
| π |
| 4 |
A、T=2π,一条对称轴方程为x=
| ||
B、T=2π,一条对称轴方程为x=
| ||
C、T=π,一条对称轴方程为x=
| ||
D、T=π,一条对称轴方程为x=
|
考点:函数y=Asin(ωx+φ)的图象变换,二倍角的余弦
专题:三角函数的图像与性质
分析:由二倍角的余弦公式降幂,化为y=Asin(ωx+φ)+b的形式,由周期公式求周期,求出对称轴方程
x=
+
,k∈Z.取k值得答案.
x=
| kπ |
| 2 |
| π |
| 4 |
解答:
解:由y=2sin2(x+
),得
y=1-cos2(x+
)=1-cos(2x+
)=1+sin2x.
∴T=
=π.
由2x=kπ+
,得x=
+
,k∈Z.
取k=1,得x=
.
∴T=π,一条对称轴方程为x=
.
故选:D.
| π |
| 4 |
y=1-cos2(x+
| π |
| 4 |
| π |
| 2 |
∴T=
| 2π |
| 2 |
由2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
取k=1,得x=
| 3π |
| 4 |
∴T=π,一条对称轴方程为x=
| 3π |
| 4 |
故选:D.
点评:本题考查二倍角的余弦公式,考查了y=Asin(ωx+φ)+b的图象和性质,是基础题.

练习册系列答案
相关题目
已知a∈R,设p:a2+3a+2≤0;q:关于x的方程x2+2x+log2a=0有实数根.则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
利用计算机在区间(0,1)上产生两个随机数a和b,则函数y=x+
-2
有零点的概率为( )
| b |
| x |
| a |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
若某几何体的三视图如图所示,则这个几何体的体积是( )


| A、5 | B、6 | C、7 | D、8 |
如图所示的圆锥的俯视图为( )


A、 |
B、 |
C、 |
D、 |
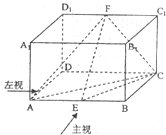 长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )
长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )