题目内容
命题p：?x∈R，x2-2x+
e2xdx＞0，则（ ）
| ∫ | 1 0 |
A、p是真命题，￢p：?x∈R，x2-2x+
| ||
B、p是假命题，￢p：?x∈R，x2-2x+
| ||
C、p是真命题，￢p：?x∈R，x2-2x+
| ||
D、p是假命题，￢p：?x∈R，x2-2x+
|
考点：命题的否定,定积分
专题：简易逻辑
分析：根据全称命题的定义和含有量词的命题的否定即可得到结论．
解答：
解：命题为全称命题，∴命题的否定是特此命题为：￢p：?x∈R，x2-2x+
e2xdx≤0．
∵x2-2x+
e2xdx=x2-2x+
e2x|
=x2-2x+
e2-
=（x-1）2+
e2-
＞0，恒成立，
∴p是真命题，
故选：C．
| ∫ | 1 0 |
∵x2-2x+
| ∫ | 1 0 |
| 1 |
| 2 |
1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴p是真命题，
故选：C．
点评：本题主要考查含有量词的命题的否定和命题真假的判断，比较基础．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
已知数列{an}中，a1=1，an+1=2an+n-1，若利用如图所示的程序框图进行运算，则输出n的值为若函数f（x）=x2+x-a，则使得“函数y=f（x）在区间（-1，1）内有零点”成立的一个必要非充分条件是（ ）
A、-
| ||
B、-
| ||
| C、0＜a＜2 | ||
D、-
|
已知函数f（x）=|lnx|，若
＞a＞b＞1，则f（a），f（b），f（c）比较大小关系正确的是（ ）
| 1 |
| c |
| A、f（c）＞f（b）＞f（a） |
| B、f（b）＞f（c）＞f（a） |
| C、f（c）＞f（a）＞f（b） |
| D、f（b）＞f（a）＞f（c） |
将函数f（x）=
sin2x+
cos2x的图象向右平移
个单位，再把横坐标扩大到原来的2倍得到函数y=g（x）的图象，下面结论正确的是（ ）
| 2 |
| 6 |
| π |
| 4 |
A、函数y=g（x）在[0，
| ||
B、函数y=g（x）图象的一个对称中心为（
| ||
C、函数y=g（x+φ）为偶函数时，其中一个φ=-
| ||
D、函数y=g（x）图象关于直线x=
|
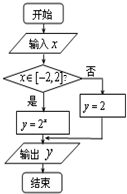
阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
已知集合A=（-1，2），集合B={x|-x2-2x+3＞0}，则A∪B=（ ）
| A、（-1，1） |
| B、（-3，2） |
| C、（-1，3） |
| D、（-1，2） |