如果执行如图所示的程序框图，则输出的S值为（ ）
| A、-3 | ||
| B、2 | ||
C、-
| ||
D、
|
若函数f（x）=asinωx-cosωx的相邻两个零点的距离为π，且它的一条对称轴为x=
π，则f（-
）等于（ ）
| 2 |
| 3 |
| π |
| 3 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
函数f（x）=log
（-x2+2x+15）的单调递增区间为（ ）
| 1 |
| 3 |
| A、（-∞，1] |
| B、[1，+∞） |
| C、[1，5] |
| D、[1，5） |
已知cosαcosβ=
，sin（
+α+β）=
，则sinαsinβ=（ ）
| 1 |
| 3 |
| π |
| 2 |
| 7 |
| 8 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如果执行如图的程序框图，输出的S=72，则判断框中为（ ）
| A、k≥9 | B、k≤8 |
| C、k≤9 | D、k≥8 |
若某人在点A测得金字塔顶端仰角为30°，此人往金字塔方向走了80米到达点B，测得金字塔顶端的仰角为45°，则金字塔的高度最接近于（忽略人的身高） （参考数据
≈1.732）（ ）
| 3 |
| A、110米 | B、112米 |
| C、220米 | D、224米 |
若函数f（x+1）=
，则f（4）=（ ）
| x | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆的方程为（x-1）2+y2=1，直线l的方程为3x+4y+m=0，若圆与直线相切，则实数m的值为（ ）
| A、2 | B、-8 | C、2或-8 | D、0 |
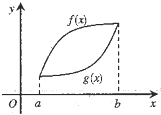已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（ ）| A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率 |
| B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率 |
| C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率 |
| D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率 |
已知曲线f（x）=
sinωx+cosωx关于直线x=
对称，当ω取最小正数时（ ）
| 3 |
| π |
| 2 |
A、f（x）在（0，
| ||||
B、f（x）在（
| ||||
C、f（x）在（-
| ||||
D、f（x）在（-
|