题目内容
已知曲线f(x)=
sinωx+cosωx关于直线x=
对称,当ω取最小正数时( )
| 3 |
| π |
| 2 |
A、f(x)在(0,
| ||||
B、f(x)在(
| ||||
C、f(x)在(-
| ||||
D、f(x)在(-
|
考点:两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用三角恒等变换,可求得f(x)=2sin(ωx+
),利用正弦函数的单调性可求得
ω+
=kπ+
(k∈Z),从而可求得ωmin=2,利用正弦函数的单调性即可求得答案.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
解答:
解:∵f(x)=
sinωx+cosωx
=2(
sinωx+
cosωx)
=2sin(ωx+
),
其图象关于直线x=
对称,
∴
ω+
=kπ+
(k∈Z),
∴ω=2k(k∈Z),又ω>0,
∴ωmin=2.
∴f(x)=2sin(2x+
),
由-
<2x+
<
,
∴-
<x<
,
∴f(x)在(-
,
)单调递增,可排除D;
又(0,
)⊆(-
,
),
∴f(x)在(0,
)单调递增,即A正确,B错误;
又(-
,0)⊆(-
,
),f(x)在区间(-
,0)上单调递增,故C错误;
故选:A.
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2sin(ωx+
| π |
| 6 |
其图象关于直线x=
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
∴ω=2k(k∈Z),又ω>0,
∴ωmin=2.
∴f(x)=2sin(2x+
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 6 |
∴f(x)在(-
| π |
| 3 |
| π |
| 6 |
又(0,
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴f(x)在(0,
| π |
| 6 |
又(-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
故选:A.
点评:本题考查两角和与差的正弦函数,着重考查正弦函数的对称性与单调性,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
设a>0,b>0,e是自然对数的底数,则( )
| A、若ea-3b=eb-2a,则a<b |
| B、若ea-3b=eb-2a,则a>b |
| C、若ea+3b=eb+2a,则a<b |
| D、若ea+3b=eb+2a,则a>b |
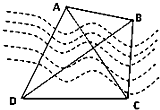 如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )
如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )A、
| ||||
B、200
| ||||
C、100
| ||||
| D、数据不够,无法计算 |
α为平面,m,n是两条不同直线,则m∥n的一个充分条件是( )
| A、m∥α且n∥α |
| B、m,n与平面α所成的角相等 |
| C、m⊥α且n⊥α |
| D、m,n与平面α的距离相等 |
如果执行如图的程序框图,输出的S=72,则判断框中为( )


| A、k≥9 | B、k≤8 |
| C、k≤9 | D、k≥8 |
若集合A={x|0≤x<1},B={x|x2<2x},则A∩B=( )
| A、{x|0<x<1} |
| B、{x|0≤x<1} |
| C、{x|0<x≤1} |
| D、{x|0≤x≤1} |
某校共有高中学生1000人,其中高一年级400人,高二年级340人,高三年级260人,现采用分层抽样抽取容量为50的样本,那么高一、高二、高三各年级抽取人数分别为( )
| A、20、17、13 |
| B、20、15、15 |
| C、40、34、26 |
| D、20、20、10 |