题目内容
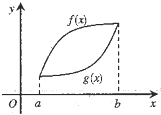 已知函数f(x)和g(x)在区间[a,b]上的图象如图所示,那么下列说法正确的是( )
已知函数f(x)和g(x)在区间[a,b]上的图象如图所示,那么下列说法正确的是( )| A、f(x)在a到b之间的平均变化率大于g(x)在a到b之间的平均变化率 |
| B、f(x)在a到b之间的平均变化率小于g(x)在a到b之间的平均变化率 |
| C、对于任意x0∈(a,b),函数f(x)在x=x0处的瞬时变化率总大于函数g(x)在x=x0处的瞬时变化率 |
| D、存在x0∈(a,b),使得函数f(x)在x=x0处的瞬时变化率小于函数g(x)在x=x0处的瞬时变化率 |
考点:变化的快慢与变化率
专题:导数的概念及应用
分析:由函数在某一区间上的平均变化率的定义,可以判定选项A、B错误;
由函数在某一点处的瞬时变化率是函数在该点处的导数,即函数在该点处的切线的斜率,可以判定选项C错误,D正确.
由函数在某一点处的瞬时变化率是函数在该点处的导数,即函数在该点处的切线的斜率,可以判定选项C错误,D正确.
解答:
解:对于A、B,∵f(x)在a到b之间的平均变化率是
,
g(x)在a到b之间的平均变化率是
,
∴
=
,即二者相等;
∴选项A、B错误;
对于C、D,∵函数f(x)在x=x0处的瞬时变化率是函数f(x)在x=x0处的导数,
即函数f(x)在该点处的切线的斜率,
同理函数g(x)在x=x0处的瞬时变化率是函数g(x)在x=x0处的导数,
即函数g(x)在x=x0处的切线的斜率,
由图形知,选项C错误,D正确.
故选:D.
| f(b)-f(a) |
| b-a |
g(x)在a到b之间的平均变化率是
| g(b)-g(a) |
| b-a |
∴
| f(b)-f(a) |
| b-a |
| g(b)-g(a) |
| b-a |
∴选项A、B错误;
对于C、D,∵函数f(x)在x=x0处的瞬时变化率是函数f(x)在x=x0处的导数,
即函数f(x)在该点处的切线的斜率,
同理函数g(x)在x=x0处的瞬时变化率是函数g(x)在x=x0处的导数,
即函数g(x)在x=x0处的切线的斜率,
由图形知,选项C错误,D正确.
故选:D.
点评:本题考查了导数的概念及其应用问题,解题时应结合平均变化率与瞬时变化率以及导数的几何意义,判定每一个选项是否正确,是基础题.

练习册系列答案
相关题目
下列命题中,与命题“函数y=
的定义域为R”不等价的命题是( )
| ax2+bx+c |
| A、函数y=ax2+bx+c的最小值大于0 |
| B、不等式ax2+bx+c≥0对任意实数恒成立 |
| C、不存在x0∈R,使ax02+bx0+c<0 |
| D、函数y=ax2+bx+c的值域是[0,+∞)的子集 |
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为( )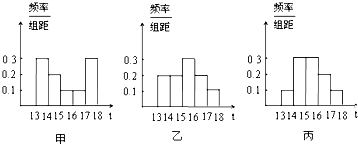

| A、s1>s2>s3 |
| B、s1>s3>s2 |
| C、s2>s3>s1 |
| D、s3>s2>s1 |
定义某种运算⊙,S=a⊙b,的运算原理如图所示,则式子6⊙3+2⊙4=( )


| A、16 | B、14 | C、10 | D、6 |
已知cosαcosβ=
,sin(
+α+β)=
,则sinαsinβ=( )
| 1 |
| 3 |
| π |
| 2 |
| 7 |
| 8 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若△ABC的三个顶点是A(-5,0),B(3,-3),C(0,2),则△ABC的面积为( )
A、
| ||
| B、31 | ||
| C、23 | ||
| D、46 |
要得到一个偶函数的图象,只需将函数f(x)=sin(x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|