甲乙两队进行排球比赛,已知在一局比赛中甲队获胜的概率是
,没有平局.若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知椭圆C:
+
=1(a>b>0)的左右焦点分别为F1,F2,若椭圆C上恰有8个不同的点P,使得△F1F2P为直角三角形,则椭圆C的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
若z∈C且z=cosα+isinα,α∈R,则|z-3-4i|的最大值是( )
| A、3 | B、4 | C、5 | D、6 |
执行如图所示的程序框图,输出的结果是15,则a的初始值m(m>0)有多少种可能( )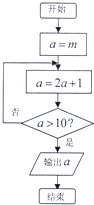

| A、1 | B、2 | C、3 | D、4 |
已知圆C:x+(y-1)2=
直线l:y=
x将l绕原点按逆时针方向旋转θ(θ为锐角)第一次与圆C相切,则tanθ的值是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=3,b=4,c=
,那么C等于( )
| 13 |
| A、30° | B、45° |
| C、60° | D、120° |
圆的标准方程为:(x-a-1)2+(y-b+2)2=r2其圆心坐标是( )
| A、(1,-2) |
| B、(-2,1) |
| C、(a+1,b-2) |
| D、(-a-1,-b+2) |
下列函数中,是奇函数的是( )
| A、y=xcosx |
| B、y=sin|x| |
| C、y=sinx+1 |
| D、y=|sinx| |
已知ξ~N(0,62),且P(0≤ξ≤2)=0.2,则P(ξ<-2)等于( )
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
若A,B是一次试验的两个事件,则“事件A,B对立”是“事件A,B互斥”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |