题目内容
若z∈C且z=cosα+isinα，α∈R，则|z-3-4i|的最大值是（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：复数求模,三角函数的最值
专题：计算题,数系的扩充和复数
分析：把z=cosα+isinα代入|z-3-4i|，利用三角恒等变换可求．
解答：
解：∵z=cosα+isinα，α∈R，
∴|z-3-4i|=|（cosα-3）+（sinα-4）i|
=
=
，
∴|z-3-4i|的最大值是
=6，
故选D．
∴|z-3-4i|=|（cosα-3）+（sinα-4）i|
=
| (cosα-3)2+(sinα-4)2 |
=
| 26-10sin(α+θ) |
∴|z-3-4i|的最大值是
| 26+10 |
故选D．
点评：该题考查复数的模、三角恒等变换，属基础题．
练习册系列答案
相关题目
用数学归纳法证明1+2+3+…+n3=
，则当n=k+1时，左端应在n=k的基础上加上（ ）
| n6+n3 |
| 2 |
| A、k3+1 | ||
| B、（k+1）3 | ||
C、
| ||
| D、（k3+1）+（k3+2）+（k3+3）+…+（k3+1）3 |
若（x+
）n展开式中第32项与第72项的系数相同，那么展开式的最中间一项的系数为（ ）
| 1 |
| x |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
在?ABCD中，错误的式子是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列函数中，是奇函数的是（ ）
| A、y=xcosx |
| B、y=sin|x| |
| C、y=sinx+1 |
| D、y=|sinx| |
如图，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ACB=β．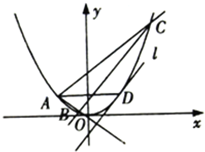
已知A，B，C，D是曲线y=x2上的四点，且A，D关于曲线的对称轴对称，直线BC与曲线在点D处的切线平行