题目内容
已知圆C:x+(y-1)2=
直线l:y=
x将l绕原点按逆时针方向旋转θ(θ为锐角)第一次与圆C相切,则tanθ的值是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:直线与圆的位置关系,圆的切线方程
专题:直线与圆
分析:由条件利用直线和圆相切的性质求出切线的斜率,再根据两条直线的夹角公式求出tanθ的值.
解答:
解:设l绕原点按逆时针方向旋转θ(θ为锐角)第一次与圆C相切时的方程为y=kx,k>0,
则由
=
,求得k=1,
再根据两条直线的夹角公式可得tanθ=
=
,
故选:A.
则由
| |0-1| | ||
|
| 1 |
| 2 |
再根据两条直线的夹角公式可得tanθ=
1-
| ||
1+1×
|
| 1 |
| 2 |
故选:A.
点评:本题主要考查直线和圆相切的性质,两条直线的夹角公式的应用,属于基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
x,y∈R,x∈[0,1],y∈[0,1],则x2≤y≤x的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x∈(-
,
),则函数y=tan(x+kπ),k∈Z与函数y=sinx的交点个数是( )
| π |
| 2 |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
若A,B是一次试验的两个事件,则“事件A,B对立”是“事件A,B互斥”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在等比数列{an}中,a4=8a1,则公比q的值为( )
| A、2 | B、3 | C、4 | D、8 |
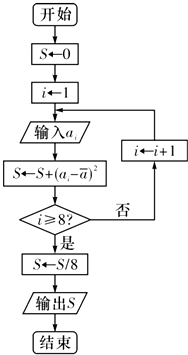 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: