题目内容

已知ξ～N（0，62），且P（0≤ξ≤2）=0.2，则P（ξ＜-2）等于（　　）
A、0.1B、0.2
C、0.3D、0.4
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：本题考查正态分布曲线的性质，随机变量ξ服从正态分布N（0，62），由此知曲线的对称轴为x=0，从而可得结论．
解答： 解：∵随机变量ξ～N（0，62），且P（0≤ξ≤2）=0.2，
∴P（ξ＜-2）=
1
2
[1-P（0≤ξ≤2）]=0.3．
故选：C．
点评：本题考查正态分布曲线的重点及曲线所表示的意义，解题的关键是正确正态分布曲线的重点及曲线所表示的意义，由曲线的对称性求出概率，本题是一个数形结合的题．
练习册系列答案
相关题目
给出下列命题：
①“m=3”是“直线（m+3）x+my-2=0与直线mx-6y+5=0互相垂直”的充要条件；
②向量
a
，
b
均为非零向量，若|
a
|=|
b
|=|
a
+
b
|，则向量
a
与
b
的夹角为
π
3
；
③若直线a，b与平面α，β满足a?α，b?β，且a∥β，b∥α，则α∥β；
④命题p：“?k∈R，直线kx+2y-3=0与圆x2+y2=4都相交”，则￢p为假命题．
其中真命题的个数为（　　）
A、0B、1C、2D、3
若用C、R和I分别表示复数集、实数集和纯虚数集，其中C为全集，那么有（　　）
A、C=R∪I
B、R∪∁CI=R
C、∁CR=C∩I
D、∁CR∩I=I
已知函数f（x）=
ax+1，x≥t
x2+ax，x＜t
，若存在实数t使得f（x）在R上为单调函数，则a的取值范围是（　　）
A、a≥0B、a＜0
C、a≤tD、a＜-t
若函数f（x）=ax+cos2x在区间[0，
π
6
]上是单调函数，则实数a的取值范围是（　　）
A、a≤0或a≥
3
B、a≥
3
C、a≥0或a≤-
3
D、a≤-
3
执行如图所示的程序框图，输出的结果是15，则a的初始值m（m＞0）有多少种可能（　　）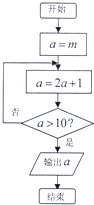
A、1B、2C、3D、4
已知函数f（x）=3x+
12
3x
（x＜0），求函数f（x）的最大值，以及取得最大值时x的值．
（Ⅰ）一个骰子投掷2次，得到的点数分别为a，b，求直线y=a-b与函数y=sinx图象所有交点中相邻两个交点的距离都相等的概率．
（Ⅱ）若a是从区间[0，6]上任取一个数，b是从区间[0，6]上任取一个数，求直线y=a-b在函数y=sinx图象上方的概率．
某高校的自主招生考试设置了自荐、笔试和面试三个环节，并规定某个环节通过后才能进入下一环节，且三个环节都通过才能被录取．某学生A三个环节依次通过的概率组成一个公差为
1
8
的等差数列，且第一个环节不通过的概率超过
1
2
，第一个环节通过但第二个环节不通过的概率为
5
32
，假定每个环节学生是否通过是相互独立的．
（Ⅰ）求学生A被录取的概率；
（Ⅱ）记学生A通过的环节数为ξ，求ξ的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网