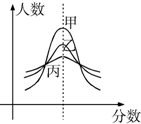
某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中正确的是（ ）| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |
已知等差数列{an}中，a2=4，a6=12，则公差d等于（ ）
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
已知f（x）=
，则f（f（-1））=（ ）
|
| A、1 | B、0 | C、-1 | D、e |
下列函数在（1，+∞）上是增函数的是（ ）
| A、y=-2x | ||
B、y=log
| ||
| C、y=-（x-1） | ||
| D、y=|x-1| |
袋中装有白球3个，黑球4个，从中任取3个，
①恰有1个白球和全是白球；
②至少有1个白球和全是黑球；
③至少有1个白球和至少有2个白球；
④至少有1个白球和至少有1个黑球．
在上述事件中，是对立事件的为（ ）
①恰有1个白球和全是白球；
②至少有1个白球和全是黑球；
③至少有1个白球和至少有2个白球；
④至少有1个白球和至少有1个黑球．
在上述事件中，是对立事件的为（ ）
| A、① | B、② | C、③ | D、④ |
如图是导函数y=f′（x）的图象，那么函数y=f（x）在下面哪个区间是减函数（ ）
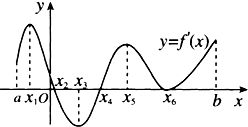
| A、（x1，x3） |
| B、（x2，x4） |
| C、（x4，x6） |
| D、（x5，x6） |
设函数f（x）=
，类比课本推导等差数列前n项和公式的推导方法计算f（-4）+f（-3）+…+f（0）+f（1）+…+f（4）+f（5）的值为（ ）
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
点P（x，y）在椭圆
+（y-1）2=1上，则x+y的最大值为（ ）
| (x-2)2 |
| 4 |
A、3+
| ||
B、5+
| ||
| C、5 | ||
| D、6 |
已知函数f（x）=
x3+ax2-4在区间（0，2）上是减函数，则a的范围是（ ）
| 1 |
| 3 |
| A、（-∞，3] |
| B、[-1，+∞） |
| C、[3，+∞） |
| D、（-∞，-1] |
在△ABC中，角A、B、C所对的边为a，b，c，若a=1，b=
，B=120°，则A等于（ ）
| 3 |
| A、30° | B、45° |
| C、60° | D、120° |