题目内容
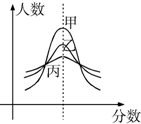某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中正确的是（ ）| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：根据正态曲线的特征进行判断，从图中看出，正态曲线的对称轴相同，最大值不同，从而得出平均数和标准差的大小关系，结合甲、乙、丙的总体即可选项．
解答：
解：由题中图象可知三科总体的平均数（均值）相等，由正态密度曲线的性质，
可知σ越大，正态曲线越扁平，σ越小，正态曲线越尖陡，
故三科总体的标准差从小到大依次为甲、乙、丙．
故选：A．
可知σ越大，正态曲线越扁平，σ越小，正态曲线越尖陡，
故三科总体的标准差从小到大依次为甲、乙、丙．
故选：A．
点评：本题主要考查了正态分布曲线的特点及曲线所表示的意义，以及数形结合的能力，属于基础题．
练习册系列答案
相关题目
下列函数在区间（-1，1）上单调递增的是（ ）
A、y=
| ||
| B、y=x2 | ||
| C、y=x3 | ||
| D、y=lnx |
已知命题p：?x∈R，ax＞0（a＞0且a≠1），则（ ）
| A、￢p：?x∈R，ax≤0 |
| B、￢p：?x∈R，ax＞0 |
| C、￢p：?x0∈R，a x0＞0 |
| D、￢p：?x0∈R，a x0≤0 |
函数f（x）=log3（2x+1）的值域为（ ）
| A、（0，+∞） |
| B、[0，+∞） |
| C、（1，+∞） |
| D、[1，+∞） |
如图是导函数y=f′（x）的图象，那么函数y=f（x）在下面哪个区间是减函数（ ）
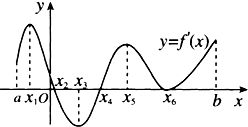
| A、（x1，x3） |
| B、（x2，x4） |
| C、（x4，x6） |
| D、（x5，x6） |
已知a=log23，b=log43.2，c=log43.6，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、c＞a＞b |
f（x）是定义在R上的偶函数，已知函数f（x）在（-∞，0]上单调递减，且f（2）=0，则使f（x）＜0的x的取值范围是（ ）
| A、（-2，0]∪[2，+∞） |
| B、（-2，2） |
| C、（-2，0） |
| D、（2，+∞） |
已知向量
，
满足：|
|=2，|
|=1，且
•
=2，则|
+
|为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | B、4 | C、9 | D、8 |
平面ABC，∠BAC=90°，F为棱AA1上的动点，A1A=4，AB=AC=2．