已知曲线C的参数方程
(t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为( )
|
A、ρ=
| ||||
B、ρsin(θ+
| ||||
C、ρsin(θ+
| ||||
D、ρ=sin(θ+
|
函数f(x)=
+mx在[1,2]上是增函数,则m的取值范围为( )
| 1 |
| x |
A、[
| ||
| B、[1,4] | ||
| C、[1,+∞) | ||
| D、(-∞,-1] |
在△ABC中,“cosA=cosB”是“sinA=sinB”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
直线
(t为参数)的倾斜角为( )
|
| A、30° | B、60° |
| C、90° | D、135° |
如果用反证法证明“数列{an}的各项均小于2”,那么应假设( )
| A、数列{an}的各项均大于2 |
| B、数列{an}的各项均大于或等于2 |
| C、数列{an}中存在一项ak,ak>2 |
| D、数列{an}中存在一项ak,ak≥2 |
若P(A)+P(B)=1,则事件A与B的关系是( )
| A、A与B是互斥事件 |
| B、A与B是对立事件 |
| C、A与B不是互斥事件 |
| D、以上都不对 |
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z=
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
| ax+by |
| c |
A、 |
B、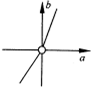 |
C、 |
D、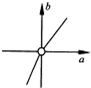 |
函数y=sin2x-sinx+2的最大值是( )
| A、2 | B、3 | C、4 | D、5 |
若cos(π-α)=-
,α∈[-
,0],则tanα=( )
| 1 |
| 3 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-2
| ||||
D、2
|