题目内容
如果用反证法证明“数列{an}的各项均小于2”，那么应假设（ ）
| A、数列{an}的各项均大于2 |
| B、数列{an}的各项均大于或等于2 |
| C、数列{an}中存在一项ak，ak＞2 |
| D、数列{an}中存在一项ak，ak≥2 |
考点：反证法与放缩法
专题：推理和证明
分析：由于用反证法证明命题时，应先假设命题的否定成立，而“数列{an}的各项均小于2”的否定为：“数列{an}中存在一项ak，ak≥2”，由此得出选项．
解答：
解：∵用反证法证明命题时，应先假设命题的否定成立，而“数列{an}的各项均小于2”的否定为：“数列{an}中存在一项ak，ak≥2”，
故选：D．
故选：D．
点评：本题主要考查用命题的否定，反证法证明数学命题的方法和步骤，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
三个平面最多可以把空间分成（ ）
| A、4部分 | B、6部分 |
| C、7部分 | D、8部分 |
下面对相关系数r描述正确的是（ ）
| A、r＞0表两个变量负相关 |
| B、r＞1表两个变量正相关 |
| C、r 只能大于零 |
| D、|r|越接近于零，两个变量相关关系越弱 |
已知F1（-3，0），F2（3，0），是椭圆
+
=1（a＞b＞0）两个焦点，P在椭圆上，∠F1PF2=α，且当α=
时，△F1PF2的面积最大，则椭圆的标准方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知曲线C的参数方程
（t为参数），C在点（1，1）处的切线为l，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则l的极坐标方程为（ ）
|
A、ρ=
| ||||
B、ρsin（θ+
| ||||
C、ρsin（θ+
| ||||
D、ρ=sin（θ+
|
若原点到直线ax+by+1=0的距离为
，则两圆（x-a）2+y2=1，x2+（y-b）2=1的位置关系是（ ）
| 1 |
| 2 |
| A、内切 | B、外切 | C、内含 | D、外离 |
如图是正方体的侧面展开图，L1、L2是两条侧面对角线，则在正方体中，L1与L2（ ）
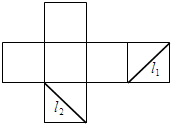
| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |