函数y=x2cos2x的导数为（ ）
| A、y′=2xcos2x-x2sin2x |
| B、y′=2xcos2x-2x2sin2x |
| C、y′=x2cos2x-2xsin2x |
| D、y′=2xcos2x+2x2sin2x |
在正方体ABCD-A1B1C1D1中，结合各棱长的中点和8个顶点，在这20个点中，任取两点构成的直线中与直线BD1
垂直的条数是（ ）
垂直的条数是（ ）
| A、18 | B、21 | C、27 | D、36 |
已知等差数列{an}的公差为2，若a3是a1与a4的等比中项，则a2=（ ）
| A、-4 | B、-6 | C、-8 | D、-10 |
函数f（x）=lgx+2x-6的零点的个数为（ ）个．
| A、0 | B、1 | C、2 | D、3 |
设全集I={1，2，3，4，5，6}，集合A，B都是I的子集，若A∩B={1，3，5}，则称A，B为“理想配集”，记作（A，B），问这样的“理想配集”（A，B）共有（ ）
| A、7个 | B、8个 |
| C、27个 | D、28个 |
已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f′（x）≥0，则a=f（
），b=f（
），c=f（
）的大小关系是（ ）
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
| A、c＜b＜a |
| B、c＜a＜b |
| C、a＜c＜b |
| D、a＜b＜c |
下面命题正确的个数是（ ）
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
| A、0个 | B、1个 | C、2个 | D、3个 |
已知不同直线m，n和不同平面α，β，给出下列命题：
①若α∥β，m?α，则m∥β；
②若m∥n，n⊥β，m?α，则α⊥β；
③若α∥m，β∥m，则α∥β；
④若α⊥β，m∥α，则m⊥β．
其中的真命题有（ ）
①若α∥β，m?α，则m∥β；
②若m∥n，n⊥β，m?α，则α⊥β；
③若α∥m，β∥m，则α∥β；
④若α⊥β，m∥α，则m⊥β．
其中的真命题有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
已知{an}是等差数列，Sn为其前n项和，若S23=S4000，O为坐标原点，P（1，a1），Q（2012，a2012），则
•
=（ ）
| OP |
| OQ |
| A、2012 | B、-2012 |
| C、0 | D、1 |
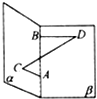如图，在120°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=5，AC=2，BD=3，则线段CD的长为（ ）