题目内容
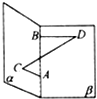如图，在120°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=5，AC=2，BD=3，则线段CD的长为（ ）A、4
| ||
B、4
| ||
C、2
| ||
D、2
|
考点：点、线、面间的距离计算
专题：综合题,空间位置关系与距离
分析：由已知可得
•
=0，
•
=0，
=
+
+
，利用数量积的性质即可得出．
| CA |
| AB |
| AB |
| BD |
| CD |
| CA |
| AB |
| BD |
解答：
解：由条件，知
•
=0，
•
=0，
=
+
+
．
因为AB=5，AC=2，BD=3，
所以|
|2=22+52+32+2×2×3cos120°=32
所以CD=4
cm，
故选：B．
| CA |
| AB |
| AB |
| BD |
| CD |
| CA |
| AB |
| BD |
因为AB=5，AC=2，BD=3，
所以|
| CD |
所以CD=4
| 2 |
故选：B．
点评：本题考查面面角，考查空间距离的计算，熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
相关题目
直线l：y=k（x+2）被圆C：x2+y2=4截得的线段长为2，则k的值为（ ）
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
某几个体的三视图如图所示，则该几何体的表面积为（ ）
| A、18 | B、21 | C、27 | D、30 |
若函数f（x）满足?m∈R，m≠0，对定义域内的任意x，f（x+m）=f（x）+f（m）恒成立，则称f（x）为m函数，现给出下列函数：
①y=
；
②y=2x；
③y=sinx；
④y=1nx
其中为m函数的个数为（ ）
①y=
| 1 |
| x |
②y=2x；
③y=sinx；
④y=1nx
其中为m函数的个数为（ ）
| A、1 | B、3 | C、4 | D、2 |
某地气象台预报“本市明天有雨的概率是95%”．以下理解正确的是（ ）
| A、本市明天将有95%的地区有雨 |
| B、本市明天将有95%的时间有雨 |
| C、明天出行不带雨具肯定会淋雨 |
| D、明天出行不带雨具淋雨的可能性较大 |
设全集I={1，2，3，4，5，6}，集合A，B都是I的子集，若A∩B={1，3，5}，则称A，B为“理想配集”，记作（A，B），问这样的“理想配集”（A，B）共有（ ）
| A、7个 | B、8个 |
| C、27个 | D、28个 |
已知函数f（x）=2x+
（x＞0，a＞0）在x=2处取得最小值，则a的值为（ ）
| a |
| x |
| A、8 | ||
| B、4 | ||
C、
| ||
| D、1 |
设集合M={x|x=
+
，k∈Z}，N={x|x=kπ±
，k∈Z}，则M、N的关系是（ ）
| kπ |
| 2 |
| π |
| 4 |
| π |
| 4 |
| A、M=N | B、M≠N |
| C、M?N | D、M?N |