题目内容
设全集I={1,2,3,4,5,6},集合A,B都是I的子集,若A∩B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
| A、7个 | B、8个 |
| C、27个 | D、28个 |
考点:子集与真子集
专题:计算题,集合
分析:A,B中都含有元素1,3,5,只要将元素2,4,6投向“篮筐”A、B,“篮球”2可能落入A中、B中或A,B之外,但不可能同时落入A、B中,同样,4和6投出后的入筐方式总数即对应理想配集的个数.
解答:
解:A,B中都含有元素1,3,5,只要将元素2,4,6投向“篮筐”A、B,“篮球”2可能落入A中、B中或A,B之外,但不可能同时落入A、B中,同样,4和6投出后的入筐方式总数即对应理想配集的个数,有3×3×3=27个.
故选:C.
故选:C.
点评:本题考查新定义,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
设椭圆
+
=1(a>b>0)的两个焦点分别为F1,F2,点P在椭圆上,且
•
=0,tan∠PF1F2=
,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是( )
| A、平行 | B、相交 |
| C、平行或相交 | D、垂直相交 |
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
命题“对任意x∈R,都有2x>0”的否定是( )
| A、对任意x∈R,都有2x≤0 |
| B、不存在x∈R,使得2x≤0 |
| C、存在x0∈R,使得2x>0 |
| D、存在x0∈R,2x0≤0 |
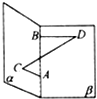 如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )
如图,在120°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=5,AC=2,BD=3,则线段CD的长为( )