题目内容
在正方体ABCD-A1B1C1D1中,结合各棱长的中点和8个顶点,在这20个点中,任取两点构成的直线中与直线BD1
垂直的条数是( )
垂直的条数是( )
| A、18 | B、21 | C、27 | D、36 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:以B为原点,BC,BA,BB1分别为x,y,z轴建立空间直角坐标系,设正方体棱长为1,BD1的坐标就是
=(1,1,1)把对于各个顶点和各棱的中点(共20个点)组成的集合记为集合E,E中的点坐标形式(x,y,z) 其中x,y,z可以取的值是{0,
,1}三者中的一个.对x分类讨论,能求出任取两点构成的直线中与直线BD1
垂直的条数.
| b |
| 1 |
| 2 |
垂直的条数.
解答:
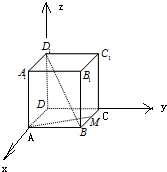 解:以B为原点,BC,BA,BB1分别为x,y,z轴建立空间直角坐标系,
解:以B为原点,BC,BA,BB1分别为x,y,z轴建立空间直角坐标系,
设正方体棱长为1
那么BD1的坐标就是
=(1,1,1)
把对于各个顶点和各棱的中点(共20个点)组成的集合记为集合E,
那么E中的点坐标形式(x,y,z) 其中x,y,z可以取的值是{0,
,1}三者中的一个.
注意到集合E中没有面对角线的交点,也没有正方体的中心,
所以上述(x,y,z)中的分量取值至多只能出现一个
,
我们把和BD1垂直的直线对应的向量记为
=(x,y,z),
即(x1-x2,y1-y2,z1-z2)
则x,y,z的取值是{0,±
,±1} 中的一个.
为了避免重复限定x≥0,下面对x分类讨论:
(1)当x=0时,要满足a⊥b,则0+y+z=0≥y+z=0,
此时y,z的取值可以是y=
,z=-
,或y=1,z=-1,或y,z取值互换的另两种情况:
①对于y=
,z=-
,则对应的直线4条,分别是:
(0,
,0)-(0,0,
)
(0,1,
)-(0,
,1)
(1,
,0)-(1,0,
)
(1,1,
)-(1,
,1)
如果y=-
,z=
,则上述4条直线中起点和终点交换位置,直线还是同一条,
所以仍然只有4条直线垂直b;
②对于y=1,z=-1 则对应的直线有3条,分别是:
(0,1,0)-(0,0,1)
(
,1,0)-(
,0,1)
(1,1,0)-(1,0,1)
同理y和z交换后直线并没有增多,仍然是3条直线垂直b,
综合(1)的情况,x=0时对应的直线有3+4=7条;
(2)当X=
时,要满足a⊥b,则
+y+z=0≥y+z=-
,
此时y,z的取值可以是y=0,z=-
,或y=
,z=-1,或y,z取值互换的另两种情况:
①对于y=0,z=-
,则对应的直线有4条,分别是:
(
,0,0)-(0,0,
)
(
,1,0)-(0,1,
)
(1,0,
)-(
,0,1)
(1,1,
)-(
,1,1)
如果y,z互换取值,那么对应的直线又多了4条,
因此这种情况下,对应的直线就有8条;
②对于y=
,z=-1,则对应的直线有2条,分别是:
(
,1,0)-(0,
,1)
(1,
,0)-(
,0,1)
同理,如果互换y,z,则对应的直线又多了2条,因此这种情况下,对应的直线就有4条
综合(2)的情况,X=
时,对应的直线就有8+4=12条;
(3)当x=1时,要满足a⊥b,则1+y+z=0≥y+z=-1,
此时y,z的取值可以是y=0,z=-1,或y=-1,z=0,或y=-
,z=-
,
①对于y=0,z=-1 则对应的直线有3条,分别是:
(1,0,0)-(0,0,1)
(1,
,0)-(0,
,1)
(1,1,0)-(0,1,1)
②对于y=-1,z=0 情况和①类似,只是交换了y,z的取值而已,因此对应直线也是3条.
③对于y=z=-
,则对应的直线有2条,分别是
(1,
,0)-(0,1,
)
(1,0,
)-(0,
,1)
综合(3)的情况,x=1时对应的直线一共有3+3+2=8条.
于是综合(1),(2),(3)和BD1垂直的直线就有7+12+8=27条.
故选:C.
 解:以B为原点,BC,BA,BB1分别为x,y,z轴建立空间直角坐标系,
解:以B为原点,BC,BA,BB1分别为x,y,z轴建立空间直角坐标系,设正方体棱长为1
那么BD1的坐标就是
| b |
把对于各个顶点和各棱的中点(共20个点)组成的集合记为集合E,
那么E中的点坐标形式(x,y,z) 其中x,y,z可以取的值是{0,
| 1 |
| 2 |
注意到集合E中没有面对角线的交点,也没有正方体的中心,
所以上述(x,y,z)中的分量取值至多只能出现一个
| 1 |
| 2 |
我们把和BD1垂直的直线对应的向量记为
| a |
即(x1-x2,y1-y2,z1-z2)
则x,y,z的取值是{0,±
| 1 |
| 2 |
为了避免重复限定x≥0,下面对x分类讨论:
(1)当x=0时,要满足a⊥b,则0+y+z=0≥y+z=0,
此时y,z的取值可以是y=
| 1 |
| 2 |
| 1 |
| 2 |
①对于y=
| 1 |
| 2 |
| 1 |
| 2 |
(0,
| 1 |
| 2 |
| 1 |
| 2 |
(0,1,
| 1 |
| 2 |
| 1 |
| 2 |
(1,
| 1 |
| 2 |
| 1 |
| 2 |
(1,1,
| 1 |
| 2 |
| 1 |
| 2 |
如果y=-
| 1 |
| 2 |
| 1 |
| 2 |
所以仍然只有4条直线垂直b;
②对于y=1,z=-1 则对应的直线有3条,分别是:
(0,1,0)-(0,0,1)
(
| 1 |
| 2 |
| 1 |
| 2 |
(1,1,0)-(1,0,1)
同理y和z交换后直线并没有增多,仍然是3条直线垂直b,
综合(1)的情况,x=0时对应的直线有3+4=7条;
(2)当X=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
此时y,z的取值可以是y=0,z=-
| 1 |
| 2 |
| 1 |
| 2 |
①对于y=0,z=-
| 1 |
| 2 |
(
| 1 |
| 2 |
| 1 |
| 2 |
(
| 1 |
| 2 |
| 1 |
| 2 |
(1,0,
| 1 |
| 2 |
| 1 |
| 2 |
(1,1,
| 1 |
| 2 |
| 1 |
| 2 |
如果y,z互换取值,那么对应的直线又多了4条,
因此这种情况下,对应的直线就有8条;
②对于y=
| 1 |
| 2 |
(
| 1 |
| 2 |
| 1 |
| 2 |
(1,
| 1 |
| 2 |
| 1 |
| 2 |
同理,如果互换y,z,则对应的直线又多了2条,因此这种情况下,对应的直线就有4条
综合(2)的情况,X=
| 1 |
| 2 |
(3)当x=1时,要满足a⊥b,则1+y+z=0≥y+z=-1,
此时y,z的取值可以是y=0,z=-1,或y=-1,z=0,或y=-
| 1 |
| 2 |
| 1 |
| 2 |
①对于y=0,z=-1 则对应的直线有3条,分别是:
(1,0,0)-(0,0,1)
(1,
| 1 |
| 2 |
| 1 |
| 2 |
(1,1,0)-(0,1,1)
②对于y=-1,z=0 情况和①类似,只是交换了y,z的取值而已,因此对应直线也是3条.
③对于y=z=-
| 1 |
| 2 |
(1,
| 1 |
| 2 |
| 1 |
| 2 |
(1,0,
| 1 |
| 2 |
| 1 |
| 2 |
综合(3)的情况,x=1时对应的直线一共有3+3+2=8条.
于是综合(1),(2),(3)和BD1垂直的直线就有7+12+8=27条.
故选:C.
点评:本题考查正方体ABCD-A1B1C1D1中,结合各棱长的中点和8个顶点的20个点中,任取两点构成的直线中与直线BD1垂直的条数的求法,解题时要认真审题,注意分类讨论思想和向量法的合理运用.

练习册系列答案
相关题目
已知数列{an}的第1项a1=1,且an+1=
(n=1,2,3,…),则数列{an}的第10项a10=( )
| an |
| 1+an |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知0<a<b,且f(x)=
-log5x,则下列大小关系式成立的是( )
| 1 |
| 5x |
A、f(b)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(a)<f(
|
已知{
,
,
}是空间的一组单位正交基底,而{
-
,
,
+
}是空间的另一组基底.若向量
在基底{
,
,
}下的坐标为(6,4,2),则向量
在基底{
-
,
,
+
}下的坐标为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| p |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| a |
| b |
| A、(1,2,5) |
| B、(5,2,1) |
| C、(1,2,3) |
| D、(3,2,1) |
下面命题正确的个数是( )
(1)若直线l上有无数个点不在平面α内,则l∥α;
(2)若直线l平行于平面α内的无数条直线,则l∥α;
(3)若直线l与平面α平行,则l与平面α内的任一直线平行;
(4)若直线l在平面α外,则l∥α.
(1)若直线l上有无数个点不在平面α内,则l∥α;
(2)若直线l平行于平面α内的无数条直线,则l∥α;
(3)若直线l与平面α平行,则l与平面α内的任一直线平行;
(4)若直线l在平面α外,则l∥α.
| A、0个 | B、1个 | C、2个 | D、3个 |
数80100除以9所得余数是( )
| A、0 | B、8 | C、-1 | D、1 |
事件A,B的概率分别为p1,p2,且p1<p2则( )
| A、P(A∩B)<p1 |
| B、P(A∪B)>p2 |
| C、P(A∪B)=p2+p1 |
| D、以上都不正确 |
已知集合P={x|x=2k,k∈Z},Q={x|x=2k+1,k∈Z},a∈P,b∈Q,则有( )
| A、(a+b)∈P |
| B、(a+b)∈Q |
| C、(a+b)∈R |
| D、以上都不对 |