函数f(x)=x+sinx(x∈R)( )
| A、是偶函数且为减函数 |
| B、是偶函数且为增函数 |
| C、是奇函数且为减函数 |
| D、是奇函数且为增函数 |
 图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )| A、8 | B、9 | C、10 | D、11 |
8个色彩不同的球平均分装在4个箱子中,现从不同的箱子中取出2个彩球,则不同的取法为( )
| A、24种 | B、12种 |
| C、6种 | D、28种 |
若函数f(x)=-x2-2x+1,则当x∈[-2,2]时,函数y=|f(x)|的值域是( )
| A、(2,7] |
| B、[-7,2) |
| C、[0,2] |
| D、[0,7] |
圆锥的中截面(过圆锥高的中点且平行于底面的截面)把圆锥侧面分成两部分,这两部分面积的比为( )
| A、1:1 | B、1:2 |
| C、1:3 | D、1:4 |
已知两条不同直线m、l,两个不同平面α、β,给出下列命题:
①若l∥α,则l平行于α内的所有直线;
②若m?α,l?β且l⊥m,则α⊥β;
③若l?β,l⊥α,则α⊥β;
④若m?α,l?β且α∥β,则m∥l;
其中正确命题的个数为( )
①若l∥α,则l平行于α内的所有直线;
②若m?α,l?β且l⊥m,则α⊥β;
③若l?β,l⊥α,则α⊥β;
④若m?α,l?β且α∥β,则m∥l;
其中正确命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(2)=4,并且对任意正整数m、n,都有f(m+n)=f(m)+f(n)成立.猜想f(n)的表达式是( )
| A、f(n)=2n |
| B、f(n)=n+2 |
| C、f(n)=2n+1 |
| D、f(n)=2n |
命题“存在x0∈R,使2x0≤0”的否定是( )
| A、不存在x0∈R,使2x0>0 |
| B、存在x0∈R,使2x0≥0 |
| C、对任意的x∈R,使2x≤0 |
| D、对任意的x∈R,使2x>0 |
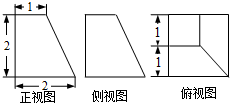 已知台体的体积公式V=
已知台体的体积公式V=