题目内容
若函数f(x)=-x2-2x+1,则当x∈[-2,2]时,函数y=|f(x)|的值域是( )
| A、(2,7] |
| B、[-7,2) |
| C、[0,2] |
| D、[0,7] |
考点:二次函数的性质
专题:函数的性质及应用
分析:首先将f(x)=-x2-2x+1的表达式变形,求出f(x)的值域,进而求出函数y=|f(x)|的值域是多少即可.
解答:
解:∵f(x)=-x2-2x+1,
∴f(x)=-(x+1)2+2;
x∈[-2,2]时,作出函数y=|f(x)|的图象,
观察图象,可以看出,|f(x)|的最小值是0,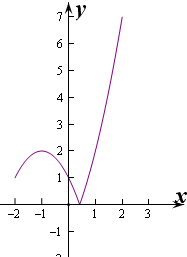
当x=2时,|f(x)|取最大值|f(2)|=|-9+2|=7;
∴函数y=|f(x)|的值域是[0,7].
故选:D.
∴f(x)=-(x+1)2+2;
x∈[-2,2]时,作出函数y=|f(x)|的图象,
观察图象,可以看出,|f(x)|的最小值是0,

当x=2时,|f(x)|取最大值|f(2)|=|-9+2|=7;
∴函数y=|f(x)|的值域是[0,7].
故选:D.
点评:此题主要考查了二次函数的性质,函数的值域的求法的运用,属于基础题,解答此题的关键是画出函数y=|f(x)|,x∈[-2,2]的图象.

练习册系列答案
相关题目
已知f(x)=
-1g
,则f(1g2)等于( )
|
| 5 |
| A、1 | ||
B、-
| ||
C、
| ||
D、
|
命题“存在x0∈R,使2x0≤0”的否定是( )
| A、不存在x0∈R,使2x0>0 |
| B、存在x0∈R,使2x0≥0 |
| C、对任意的x∈R,使2x≤0 |
| D、对任意的x∈R,使2x>0 |
已知两个定点分别为F1(-5,0),F2(5,0),动点P到F1,F2距离差的绝对值等于6,则动点P的轨迹对应的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a=(
)
,b=(
)
,c=(
)
,则a,b,c的大小关系是( )
| 3 |
| 5 |
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<c<b |
一个容量为20的数据样本,分组与频数为:[10,20]2个,(20,30]3个,(30,40]4个,(40,50]5个,(50,60]4个,(60,70]2个,则样本数据在区间(-∞,50)上的可能性为( )
| A、5% | B、25% |
| C、50% | D、70% |
函数f(x)=
的定义域为( )
| 1 |
| ln(x+1) |
| A、(-1,0)∪(0,+∞) |
| B、[-1,0)∪(0,+∞) |
| C、[-1,+∞) |
| D、(-1,+∞) |
 如图的三角形数阵中,满足:(1)第1行的数为1;(2)第n(n≥2)行首尾两数均为n,其余的数都等于它肩上的两个数相加,则第25行中第2个数是
如图的三角形数阵中,满足:(1)第1行的数为1;(2)第n(n≥2)行首尾两数均为n,其余的数都等于它肩上的两个数相加,则第25行中第2个数是