题目内容

圆锥的中截面（过圆锥高的中点且平行于底面的截面）把圆锥侧面分成两部分，这两部分面积的比为（　　）
A、1：1B、1：2
C、1：3D、1：4
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：设原圆锥侧面展开扇形的半径为R，圆心角的度数为n′，可得AP=
1
2
AC=
1
2
R，根据扇形的面积公式求得大小圆锥的侧面面积后比较，即可得到圆锥的侧面积与所得圆台的侧面积之比．
解答： 解：如图所示，设原圆锥侧面展开扇形的半径为R，圆心角的度数为n′．
∴小圆锥的半径AP=
1
2
AC=
1
2
R，
于是S1=
nπ(
1
2
R)2
360
=
1
4
•
nπR2
360
，S2=
nπR2
360
，
∴S1=
1
4
S2．圆锥的侧面积与所得圆台的侧面积之比为 1：3．
故选：C．
点评：本题是基础题，考查圆锥的侧面积与所得圆台的侧面积的求法，考查空间想象能力，计算能力．
练习册系列答案
相关题目
已知f（x）是定义在R上的增函数，且对于任意x∈R，都有f[f（x）-2x]=3，则f（3）=
 
．
已知实数x，y满足
3
x+y=|a-2|
y=
9-x2
，则不等式2|1-a|-1＞a（a-2）成立的概率是（　　）
A、
1
4
B、
1
3
C、
2
3
D、
3
4
已知命题p：?x∈R，2x=5，则￢p为（　　）
A、?x∉R，2x=5
B、?x∈R，2x≠5
C、?x0∈R，2 x0=5
D、?x0∈R，2 x0≠5
各项均不为0的等差数列{an}满足：an-1+an+1-an2=0（n∈N*，n≥2）；记该数列的前n项积为Tn，则使得不等式log3Tn＞4成立的最小正整数n为（　　）
A、5B、6C、7D、8
已知数列{an}、{bn}的通项公式分别是an=a+（n-1）d，bn=a-（n-1）d，若
a1+a3+b4≤6
b3≥-8
a6+b5≥4
，则a5+b6的最大值为（　　）
A、4B、-4C、2D、3
在锐角△ABC中，C=
π
4
，则tanA+tanB的最小值为（　　）
A、3+2
2
B、2+2
2
C、2
2
-2
D、2
2
-1
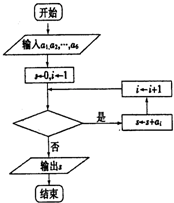如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填（　　）
A、i≤5或i＜6
B、i≤6或i＜7
C、i≥6或i＞5
D、i≥5或i＞4
过双曲线x2-y2=4的左焦点F1有一条弦PQ在左支上，若|PQ|=7，F2是双曲线的右焦点，则△PF2Q的周长是（　　）
A、8B、15C、26D、22

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网