题目内容
8个色彩不同的球平均分装在4个箱子中,现从不同的箱子中取出2个彩球,则不同的取法为( )
| A、24种 | B、12种 |
| C、6种 | D、28种 |
考点:计数原理的应用
专题:排列组合
分析:把每个色彩按1到8编号,分四组12,34,56,78,从每组种任取1个,再从剩下的一组再取一个,根据分步计数原理可得.
解答:
解:把每个色彩按1到8编号,分四组12,34,56,78,从每组种任取1个,再从剩下的一组再取一个,
•
•
•
=48种,
但是48种取法每次都有重复的颜色,即13跟31抽的颜色一样,
所以48÷2=24种色彩搭配.
故选:A.
| C | 1 4 |
| C | 1 2 |
| C | 1 3 |
| C | 1 2 |
但是48种取法每次都有重复的颜色,即13跟31抽的颜色一样,
所以48÷2=24种色彩搭配.
故选:A.
点评:本题主要考查了分步计数原理,关键是注意有重复的现象,属于基础题.

练习册系列答案
相关题目
已知直线l与过点M(-
,
)、N(
,-
)的直线垂直,则直线l的倾斜角是( )
| 3 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的焦距是( )
| x2 |
| 12 |
| y2 |
| 4 |
| A、8 | ||
| B、4 | ||
C、2
| ||
| D、2 |
已知p:|2x-3|<1,q:x(x-3)<0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=x-ln(1+x)的单调递增区间为( )
| A、(-1,0) |
| B、(-∞,-1)和(0,+∞) |
| C、(0,+∞) |
| D、(-∞,-1) |
在△ABC中,tanA=-1,C=30°,BC=2
,则AB等于( )
| 2 |
| A、4 | B、3 | C、2 | D、1 |
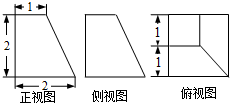 已知台体的体积公式V=
已知台体的体积公式V=