Question

已知台体的体积公式V=

1

3

（S₁+

S1S2

+S₂）h，其中S₁，S₂分别是台体上，下底的面积，h表示台体的高．某四棱台的三视图如图所示，则该四棱台的体积是（　　）

• A、

  14

  3

• B、4
• C、

  16

  3

• D、6

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：计算题,数形结合

分析：利用三视图画出直观图，代人公式V=

1

3

（S₁+

S1S2

+S₂）h计算．

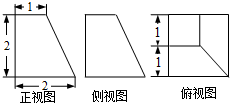
解答： 解：由题意知，得直观图如右图，HD垂直上下底面，S₁=1，S₂=4，h=2，
V=

1

3

（S₁+

S1S2

+S₂）h=

1

3

×(1+

1×4

+4)×2=

14

3

故选：A

点评：本题考查三视图及棱台的体积，关键能有三视图画出直观图，明确相应的数量及位置关系，熟悉公式，属基础题．