设函数f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意的x∈[a,b],都有|f(x)-g(x)|≤k(k>0),则称f(x)与g(x)在[a,b]上是“k度和谐函数”,[a,b]称为“k度密切区间”.设函数f(x)=lnx与g(x)=
在[
,e]上是“e度和谐函数”,则m的取值范围是( )
| mx-1 |
| x |
| 1 |
| e |
| A、[-e-1,1] | ||
| B、[-1,e+1] | ||
C、[
| ||
D、[
|
将函数y=sin2x的图象向上平移1个单位长度,再向右平移1个单位长度,所得图象对应的函数解析式是( )
| A、y=2cos2x |
| B、y=2sin2x |
| C、y=1+sin2(x-1) |
| D、y=1+sin2(x+1) |
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)≥f(x),对任意正数a,b,若a<b,则必有( )
| A、af(a)≤bf(b) |
| B、bf(a)<af(b) |
| C、af(a)>bf(b) |
| D、bf(a)≥af(b) |
数列{an}满足a1=1,a2=2,an+2=(1+cos2
)an+sin2
,n∈N*,设bn=
,Sn=b1+b2+…+bn,则Sn+
=( )
| nπ |
| 2 |
| nπ |
| 2 |
| a2n-1 |
| a2n |
| n+2 |
| 2n |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、1+
|
函数f(x)=
的定义域为( )
| 2x2-12x+10 |
| A、[5,+∞) |
| B、(-∞,1)∪(5,+∞) |
| C、(-∞,1]∪[5,+∞) |
| D、[1,5] |
已知等比数列{an}的公比q<0,其前n项和为Sn,则a10S9与a9S10的大小关系是( )
| A、a10S9>a9S10 |
| B、a10S9<a9S10 |
| C、a10S9=a9S10 |
| D、a10S9与a9S10的大小关系与a1的值有关 |
已知
=(1,2),
=(-1,m),若
与
夹角为钝角,则m的取值范围是( )
| a |
| b |
| a |
| b |
A、(-
| ||
B、(-∞,-
| ||
C、(
| ||
D、(-∞,-2)∪(-2,
|
设等差数列{an}的前n项和为Sn,已知S2+S6=0,a4=1,则a5=( )
| A、-2 | B、-1 | C、0 | D、2 |
在长为12的线段AB上任取一点M,并以线段AM为边作正三角形.此正三角形的面积介于9
与16
之间的概率( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
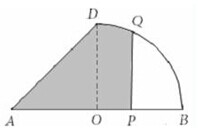 如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )
如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )


